Средние величины

  1. Средняя арифметическая

а) для дискретного ряда: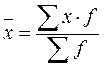

б) для интервального ряда:

где х’ – середина соответствующего интервала, вычисленная как средняя из границ интервала:

2. Медианасоответствует варианту, стоящему в середине совокупности. Положение медианы определяется ее номером: , где n – число единиц в совокупности. Численное значение медианы в ранжированном дискретном ряду с нечетным количеством единиц равно значению варьируемого признака, соответствующего найденному номеру (положению) медианы в ряду:

Если в дискретном ряду четное количество единиц, то численное значение медианы определяют как: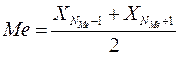

В интервальном ряду численной значение медианы определяют с помощью накопленной частоты: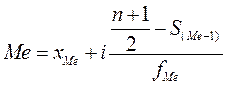

где xMe – нижняя граница медианного интервала

i – величина медианного интервала

S(Me-1) - накопленная частота интервала, предшествующего медианному

fMe – частота медианного интервала

3. Мода- величина варьируемого признака, чаще всего встречающаяся в данном ряду распределения, то есть имеющая наибольшую частоту. Численное значение моды определяется значением признака с наибольшей частотой – для дискретного ряда, а для интервального ряда следующим образом: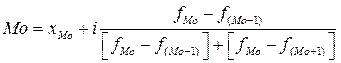

где xMo – нижняя граница модального интервала

fMo – частота модального интервала

f(Mo-1) – частота интервала, предшествующего модальному

f(Mo+1) – частота интревала, следующего за модальным

 

4. Среднее линейное отклонение:

Для не сгруппированных данных: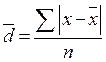

Для вариационного ряда:

Для интервального ряда: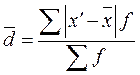

5. Среднеквадратическое отклонение:

а) Для не сгруппированных данных: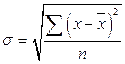

Дисперсия: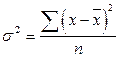

б) Для вариационного ряда: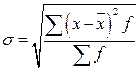

Дисперсия: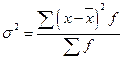

в) Для интервального ряда:

Дисперсия:

Существуют упрощенные формулы для расчета дисперсии:

а) по средним: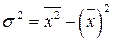

б) по частостям: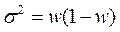

Для сравнительной оценки вариации и характеристики однородности совокупности применяют коэффициент вариации: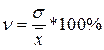

Совокупность считается однородной, если коэффициент вариации не превышает 33 %.