ЭЛЕМЕНТЫ КОМБИНАТОРИКИ

ВЕРОЯТНОСТЬ ПО ЛАПЛАСУ (Классическая вероятность)

Определение 5. Классическое определение вероятности. (Лаплас) Пусть для эксперимента со случайным исходом можно указать N событий A₁, A₂, ... , A_N, обладающих следующими свойствами:

1) события A₁, ... , A_N попарно несовместны, т.е. любые два из них не могут произойти вместе;

2) события A₁, ... , A_N образуют полную группу, т.е. при любом исходе эксперимента хотя бы одно из них непременно происходит (единственно возможные события);

3) события A₁, ... , A_N равновозможны, т.е. ни одно из них не является более предпочтительным, чем другое.

В этой классической схеме события A₁,A₂,...,A_N называют случаями, элементарными событиями или исходами. Тогда для вероятности любого случайного события А, связанного с данным экспериментом со случайным исходом, имеем (по определению): (1)

Вероятность события А равна отношению числа М благоприятных исходов, то есть тех исходов, появление которых влечёт за собой появление события А, к общему числу N всех возможных исходов.

Определение 6. Пространством элементарных событий W (исходов) называется множество N всех элементарных событий (исходов) {w₁, …w_{n …}}. Пространство элементарных событий может содержать конечное, счетное и даже бесконечное множество элементарных событий.

Определение 7. Случайным событием (событием)называется подмножество пространства элементарных событий. Элементами события являются элементарные события, образующие это событие.

Пример. Бросается одна монета, она может упасть гербом (w₁=Г) или решкой (w₁=Р). W=(Г,Р). Ясно, что

Пример. Бросание кубика: Можно по-разному перечислять исходы такого опыта.

1 способ: выпадает 6 или выпадает не 6. Исход «выпадает не 6»не элементарный, его можно разложить на совокупность более простых: «выпадает 1»или2,или3, 4, 5. Кроме того, они и не равновозможны: на кубике только одна грань с цифрой 6 и пять граней с не шестеркой.

2 способ: выпадает четное число или выпадает нечетное число. Исходыне элементарные (оба), но равновозможные: на кубике три грани с нечетным числом очков и три с четным.

3 способ: выпадает 1,или 2, или 3, или 4, или 5, или 6. Исходы и элементарны и равновозможны. Число таких исходов равно 6.

Пример:Найти вероятность того, что при бросании 2х кубиков сумма очков окажется не более 3.

Каждый элементарный исход – это пара чисел. Выпадает некоторое число на первом кубике и некоторое на втором: w_i =( число; число); На первом кубике 6 вариантов, на втором тоже. Любое число очков на первом кубике сочетается с любым числом очков на втором, т.е., n = 6 ∙ 6 =36. Событие А – сумма очков не более трех. Благоприятствующие исходы w₁ =( 1;1); w₂ =( 1;2 ); w₃ =( 2;1 ) ,

Комментарий 1. Недостатки Модели Лапласа: 1) Вероятность определяется через равновероятность. 2) Часто непонятно, что в конкретных случаях считать исходами.

Комментарий 2. В классической модели теории вероятностей существует несколько схем рассуждений.

Про опыт, в котором можно выделить случаи (исходы) говорят, что он сводится к схеме случаев. Например, опыт «бросание монеты» сводится к схеме случаев, так как события: А1 - выпадение орла и А2 - выпадение решки несовместны, образуют полную группу и равновозможны. Опыт «бросание игральной кости» тоже сводится к схеме случаев; в нем шесть несовместных, образующих полную группу и равновозможных исходов, которые можно перенумеровать по числу выпавших очков: А„ А2, А3,А4, А5, А6.

При сведении задачи к схеме случаев надо быть осторожным. Вот две известных задачи:Парадокс Даламбера: В опыте «бросание двух монет» очевидны события: В1 - выпадение двух орлов; B2 - выпадение двух решек; В3, - выпадение одного орла и одной решки. То есть все эти события имеют одинаковую вероятность и должны появляться одинаково часто. Но В3 появляется чаще.Они не случаи, так как они не равновозможны. Событие В3 вдвое более вероятно, чем каждое из остальных. Перечислим случаи для нашего опыта: А1 - орёл на первой монете и орёл на второй; А2 - решка на первой монете и решка на второй; А3 - орёл на первой монете и решка на второй; А4, - решка на первой монете и орёл на второй. События В1 и В2 совпадают с А1 и А2. А вот событие B3 распадается на два варианта: АЗ и А4, поэтому оно вдвое вероятнее каждого из остальных.

Парадокс Кардано. При бросании двух “правильных” костей подсчитывается сумма выпавших чисел. Как 9, так и 10 можно получить двумя разными способами: 9 = 3 + 6 = 4 + 5 и 10 = 4 + 6 = 5 + 5. Почему тогда 9 появляется чаще, когда бросают две кости, а 10, когда бросают три? Необходимо учесть порядок выпадения чисел (в противном случае не все исходы были бы равновозможными). В случае двух костей 9 и 10 могут быть получены соответственно 4 и 3 способами: 9 = 3+6 = 6+3 = 4+5 = 5+4 и 10 = 4+6 = 6+4 = 5+5. Если “выбрасывать” 3 кости, ситуация меняется на противоположную: 9 можно “выбросить” 25 способами, а 10 уже 26 способами.

Вторая популярная схема – схема урн. Практически каждую задачу теории вероятностей, в которой опыт сводится к схеме случаев, можно свести к той или иной задаче, где речь идет о вынимании шаров из урн. «Задачи на урны» являются своего рода единым языком, на котором можно излагать самые разнообразные по внешней форме задачи. Инструмент, при помощи которого такие задачи решаются, называется комбинаторика.

 

Комбинаторикой (от латинского combinare - соединять) называют раздел математики, в котором изучаются задачи на подсчёт количества комбинаций, удовлетворяющих тем или иным условиям, которые можно составлять из элементов данного множества. В этом смысле комбинаторика - это часть теории множеств. Комбинаторные методы находят широкое применение внутри самой математики. Это и дискретная математика и линейное программирование и теория вероятностей и математическая статистика и алгебра и геометрия и теория управления и теория информации, в частности, проблема создания надежных шифров и, наоборот, создание эффективных методов декодирования. Они также эффективны и в приложениях математики в технике и естествознании (разработка сетей компьютеров, составление расписаний, контроль качества продукции и так далее.).

 

1. ПРИНЦИПЫ КОМБИНАТОРИКИ. B основе решения комбинаторных задач лежат два принципа: - принцип суммы и принцип произведения.

1.1. Принцип суммы. Если существует m способов выбрать элемент a и (независимо от них) n способов выбрать элемент b, то выбор a или b можно сделать m + n способами. Например, если в группе 7 мальчиков и 9 девочек, то выбор “мальчик или девочка” можно сделать 16 способами - выбрать либо одного из 7 мальчиков, либо одну из 9 девочек.

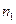1.2.Принцип произведения.Если элемент можно выбрать способами, а после него и независимо от него элемент а₂ - n₂ способами, элемент a_k - n_k сnособами, то набор (а₁,.., a_k ) можно выбратъ сnособами. Например, если в нашем распоряжении m способов выбрать элемент a и n способов выбрать элемент b, то пару (а, b) можно выбрать mn способами. Таким образом, пару “мальчик и девочка” можно выбрать способами. Ещё пример: Сколькими способами можно поставить на шахматную доску белyю и чёрную ладью так, чтобы они не били друг друга? Поле для белой ладьи можно выбрать 64 способами. Независимо от этого выбора, ладья бьёт 15 полей, поэтомy для черной ладьи остается 64 - 15= 49 пoлей. В более сложном случае надо сначала выбрать элемент а, а потом, в зависимости от этого выбора, элемент b. Но если элемент а можно выбрать m способами, а после каждого такого выбора элемент b можно выбрать n способами, то число различных пар (а,b) опять равно mn. С помощью правил суммы и произведения можно решать любые задачи комбинаторики. Но это не удобно, это всё равно, что сводить решение любой геометрической задачи к аксиомам. Поэтому в комбинаторике есть несколько простейших, стандартных задач, к которым часто удается свести решение других задач.