ЛЕКЦИЯ 4

ТЕМА: РАВНОСИЛЬНЫЕ ФОРМУЛЫ АЛГЕБРЫ ЛОГИКИ. ЗАКОНЫ ЛОГИКИ.

ПЛАН:

1. Равносильные формулы алгебры логики.
2. Важнейшие равносильности алгебры логики.
3. Равносильные преобразования формул.

Главная

 

1. Равносильные формулы алгебры логики.

Рассмотрим примеры:

2х + 4у = 2(х + 2у) – это тождество или равносильность, т.к. истинно при любых х и у;

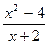, сократим дробь, получим - получившееся равенство не является тождеством, т.к. верно не при всех х и у: при х = -2 оно не верно, т.к. х = -2 не входит в область допустимых значений дроби.

Теперь рассмотрим понятие равносильных формул в математической логике.

Определение. Две формулы алгебры логики А и В называются равносильными, если они принимают оди­наковые логические значения на любом наборе значе­ний входящих в формулы элементарных высказыва­ний.

Равносильность формул будем обозначать знаком º , а запись А º В означает, что формулы А и В рав­носильны.

Например, равносильны формулы:

(Проверьте самостоятельно).

Все формулы алгебры логики можно подразделить на три класса: тавтологии, тождественно ложные и выполнимые.

Формула А называется тождественно истинной (или тавтологией) , если она принимает значение 1 при всех значениях входящих в нее переменных.

Например, тожественно истинны формулы :

(Проверьте с помощью таблицы истинности).

Формула А называется тождественно ложной, если она принимает значение 0 при всех значениях входящих в нее переменных.

Например, тождественно ложна формула

Формула А называется выполнимой, если она принимает значения и 0 и 1.

Например, формула х®у выполнимая.

Между понятиями равносильности и эквивалентно­сти существует следующая связь: если формулы А и В равносильны, то формула А « В - тавтология, и обрат­но, если формула А « В — тавтология, то формулы А и В равносильны.

Важнейшие равносильности алгебры логики можно разбить на три группы.