Волгодонск

КУРС ЛЕКЦИЙ

Российской Федерации

Министерство образования и науки

Анализ платежеспособности по краткосрочным обязательствам

В оценке платежеспособности предпрятия по краткосрочным обязательствам используют три относительных показателя ликвидности. При расчете этих показателей рассматривают различные по составу ликвидные средства в качестве покрытия краткосрочных обязательств.

 

1. Коэффициент абсолютной ликвидности К_ал =А1/(П1+П2), норма К_ал >0,2.

Показывает, какую часть краткосрочной задолженности предприятие может погасить в ближайшее время, отражает платежеспособность на дату составления баланса.

Значения этого показателя представляют интерес для поставщиков.

 

2. Коэффициент критической ликвидности _Ккл =(А1+А2)/(П1+П2), норма К_ал >1.

Отражает прогнозируемые платежные возможности предприятия при условии своевременного возврата дебиторской задолженности, характеризует платежеспособность предприятия на период равный средней продолжительности одного оборота дебиторской задолженности.

 

Значения этого показателя представляют интерес для кредитующего банка.

3. Коэффициент текущей ликвидности _Ктл =(А1+А2+А3)/(П1+П2), норма К_ал >2.

Показывает платежные возможности предприятия при условии не только своевременного расчета с дебиторами, благоприятной реализации готовой продукции, а также продажи прочих элементов материальных оборотных средств. Характеризует платежеспособность предприятия на период равный средней продолжительности одного оборота всех оборотных средств.

 

Расчет показателей ликвидности

Наименование показателя	Формула	Начало периода (расчет)	Конец периода (расчет)

 

Вывод:____________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

 

Федеральное государственное бюджетное

образовательное учреждение

высшего профессионального образования

Национальный исследовательский ядерный университет «МИФИ»

 

Волгодонский инженерно-технический институт – филиал НИЯУ МИФИ

 

 

по дисциплине

«линейное программирование»

для студентов специальности 230201

«Информационные системы и технологии»

всех форм обучения

 

 

УДК 519.8 (075.8)

Рецензент д.т.н., профессор А. В. Чернов

 

 

Составитель ст. преп. Цуверкалова О.Ф.

 

Методические указания содержат курс лекций по дисциплине «Линейное программирование» /ВИТИ НИЯУ МИФИ. Волгодонск, 2010. 93 с.

 

Предназначены для студентов очной, очно-заочной и заочной формы обучения специальности 230201 – Информационные системы и технологии

 

 

ã ВИТИ НИЯУ МИФИ, 2010

ã О.Ф. Цуверкалова, 2010

 

 

ВВЕДЕНИЕ

 

Многие задачи, с которыми приходится иметь дело в повседнев­ной практике, являются многовариантными. Среди множе­ства возможных вариантов в условиях рыночных отно­шений приходится отыскивать наилучшие варианты с учетом ограничений, налагаемых на природные, эко­номические и технологические возможности. До недавнего времени большинство таких задач решалось исходя из здравого смысла и опыта лиц, принимающих решения, или просто «на глаз». При таком подходе не было и не могло быть никакой уверенности, что найденный ва­риант – наилучший. При современных масштабах произ­водства даже незначительные ошибки оборачиваются громадными потерями. В связи с этим возникла необхо­димость применять для анализа и синтеза экономических и технологических ситуаций и систем математические методы. Такие методы объединяются под общим названием «математическое программирование».

Математическое программирование – область мате­матики, разрабатывающая теорию и численные методы решения многомерных экстремальных задач с ограниче­ниями, т. е. задач на экстремум функции многих пере­менных с ограничениями на область изменения этих переменных.

Функцию, экстремальное значение которой нужно найти в условиях экономических возможностей, называют целевой, показателем эффективности или критерием опти­мальности. Ограничения, накладываемые на область изменения переменных, формализуются в виде системы ограничений. Все это составляет матема­тическую модель.

Модель задачи математического программирования включает:

1) совокупность неизвестных величин х = (х₁, …, х_j, …, х_n), действуя на которые систему можно совершенствовать. Их называют планом задачи (вектором управления, решением, управлением, стратегией и др.);

2) целевую функцию (функцию цели, показатель эф­фективности, критерий оптимальности, функционал зада­чи и др.). Целевая функция позволяет выбирать наилуч­ший вариант из множества возможных. Наилучший ва­риант доставляет целевой функции экстремальное значе­ние. Целевую функцию обозначают буквой Z или F (Z = z(х), F = f(x)). Это может быть прибыль, объем выпуска или реализации, затраты производства, издержки обращения, уровень об­служивания или дефицитности, число комплектов, отходы и т. д.;

3) условия (или систему ограничений), налагаемые на неизвестные величины. Эти условия следуют из огра­ниченности ресурсов, которыми располагает общество в любой момент времени, необходимости удовлетворения насущных потребностей, условий производственных и технологических процессов. Ограниченными являются не только материальные, финансовые и трудовые ресурсы. Таковыми могут быть возможности технического, техноло­гического и вообще научного потенциала. Нередко по­требности превышают возможности их удовлетворения. Математически ограничения выражаются в виде уравне­ний и неравенств. Их совокупность образует область до­пустимых решений (область экономических возможно­стей). Объединение всех условий (ограничений), нала­гаемых на неизвестные (искомые) величины x_j задачи, обозначим Ω (х Î Ω). При таких обозначениях модель задачи математического программирования примет вид:

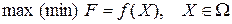или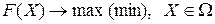

Из экономических или физических соображений на план задачи или некоторые его компоненты (координаты), как правило, налагаются условия неотрицательности, иногда – целочисленности.

План х, удовлетворяющий системе ограничений задачи, называется допустимым. Допустимый план, доставляющий функции цели экстремальное значение, на­зывается оптимальным. Оптимальный план будем обозна­чать х*, экстремальное значение функции цели – f(х*) = F*. Оптимальное решение, вообще говоря, не обяза­тельно единственно, возможны случаи, когда оно не су­ществует, имеется конечное или бесчисленное множество оптимальных решений.

В зависимости от особенностей целевой функции и функций, задающих ограничения, задачи математического программирования делятся на ряд типов.

Если целевая функция и функции, входящие в систему ограничений, линейны относительно входящих в задачу неиз­вестных, то такой раздел математического программи­рования называется линейным программированием (ЛП). Методы и модели линейного программирования широко применяются при оптимизации процессов во всех отраслях народного хозяйства: при разработке производственной программы предприятия, распределении ее по исполните­лям, при размещении заказов между исполнителями и по временным интервалам, при определении наилучшего ассортимента выпускаемой продукции, в задачах перспек­тивного, текущего и оперативного планирования и управ­ления; при планировании грузопотоков, определении плана товарооборота и его распределении; в задачах раз­вития и размещения производительных сил, баз и складов систем обращения материальных ресурсов и т. д. Особенно широкое применение методы и модели линейного програм­мирования получили при решении задач экономии ресур­сов (выбор ресурсосберегающих технологий, составление смесей, раскрой материалов), транспорт­ных и других задач.

Начало линейному программированию было положено в 1939 г. советским математиком-экономистом Л. В. Кан­торовичем в работе «Математические методы организации и планирования производства». Появление этой работы открыло новый этап в применении математики в эконо­мике. Спустя десять лет американский математик Дж. Данциг разработал эффективный метод решения данного класса задач – симплекс-метод. Термин «линейное про­граммирование» впервые появился в 1951 г. в работах Дж. Данцига и Т. Купманса.

Однако при более глубоком исследовании в ряде задач появляются и связи нелинейного характера, когда с изме­нением одного элемента другие изменяются непропорцио­нально первому. Поэтому вслед за разработкой моделей линейного программирования начались интенсивные исследования нелинейных моделей.

Если в задаче математического программирования це­левая функция и (или) хотя бы одна из функций системы ограничений нелинейна, то такой раздел называется нелинейным программированием (НЛП).

Если на все или некоторые переменные x_j наложено условие дискретности, например, целочисленности, то такие задачи рассматриваются в разделе ма­тематического программирования, называемом дискрет­ным, в частности целочисленным (ЦП), программирова­нием. Если параметры целевой функции и (или) системы ограничений изменяются во времени или целевая функция имеет аддитивный либо мультипликативный вид, или сам процесс выработки решения имеет многошаговый характер, то такие задачи решаются методами динамического программирования (ДП). Методами ДП могут ре­шаться задачи перспективного и текущего планирования, управления производством, поставками и запасами в условиях изменяющегося спроса, распределения ограниченных ресурсов, в частности размещения капитальных вложений, замены оборудования, обновления и восстановления элементов сложных человеко-машинных организационных си­стем и т. д.

В перечисленных выше разделах математического про­граммирования предполагается, что вся информация о протекании процессов заранее известна и достоверна. Та­кие методы оптимизации называются детерминированны­ми или методами обоснования решений в условиях опре­деленности.

Если параметры, входящие в функцию цели, или огра­ничения задачи являются случайными, недостоверными величинами или если приходится принимать решения в условиях риска, неполной или недостоверной информа­ции, то говорят о проблеме стохастической оптимизации, а соответствующий раздел называется стохастическим программированием (СП). К нему в первую очередь сле­дует отнести методы и модели выработки решений в усло­виях конфликтных ситуаций (математическая теория игр), в условиях неполной информации (экспертные оценки), в условиях риска (статистические решения) и др. Позднее появились другие типы задач, учитывающих специфику целевой функции и системы ограничений, в связи с чем возникли параметрическое, дробно-линейное, блочное, се­тевое (потоковое), многоиндексное, булевское, комбина­торное и другие типы программирования. В случае нелинейностей специфика задач породила квадратичное, биквадратичное, сепарабельное, выпуклое и другие типы программирования. Появились численные методы отыска­ния оптимальных решений: градиентные, штрафных и барьерных функций, возможных направлений, линейной аппроксимации, случайного поиска и др.

К математическому программированию относятся также методы решения экстремальных задач с бесконечным числом переменных - бесконечномерное программиро­вание.

И, наконец, отметим, что задачи математического программирования с одной целевой функцией решаются ме­тодами скалярной оптимизации. Однако реальные ситуа­ции настолько сложны, что нередко приходится одновре­менно учитывать несколько целевых функций, которые должны принимать экстремальные значения. Задачи, где находят решение по несколь­ким целевым функциям, относятся к векторной оптими­зации - это так называемые задачи многокритериального подхода.

Тем не менее, несмотря на многообразие оптимизационных моделей и методов, в данном пособии мы ограничимся рассмотрением задачи линейного программирования и близких к ней вопросов, поскольку этот класс задач является одним из наиболее изученных, и вместе с тем позволяет получить полное представление о математическом моделировании.