Червячные передачи
Принцип действия и область применения. Червячная передача (рисунок 11.19) относится к передачам зацепления с перекрещивающимися осями валов. Угол перекрещивания обычно равен 90°. Движение в червячных передачах преобразуется по принципу винтовой пары или по принципу наклонной плоскости. Червячная передача состоит из винта, называемого червяком (рисунок 11.20), и зубчатого колеса, называемого червячным колесом (рисунок 11.22). При вращении червяка вокруг своей оси его витки перемещаются вдоль образующей своей цилиндрической поверхности и приводит во вращательное движение червячное колесо. Червяк и червячное колесо изготовляются методом нарезания зубьев при помощи специального инструмента из целых заготовок. В червячной передаче так же, как и в зубчатой, имеются диаметры делительных цилиндров (рисунок 11.19): d1 – делительный диаметр червяка, d2 – делительный диаметр червячного колеса. Точка касания делительных диаметров называется полюсом зацепления.
Рисунок 11.19 – Схема червячной передачи.
Достоинства червячных передач:
1. Возможность получения большого передаточного числа в одной ступени (i = 8 – 200).
2. Плавность и бесшумность работы.
3. Компактность (малые габариты).
4. Самоторможение (невозможность передачи вращающего момента от червячного колеса к червяку).
5. Демпфирующие свойства снижают уровень вибрации машин.
Недостатки червячных передач:
1. Значительное трение в зоне зацепления.
2. Нагрев передачи.
3. Низкий КПД.
Червячные передачи используются в устройствах с ограниченной мощностью (обычно до 50 кВт).
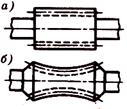
Рисунок 11.20 – Червяки.
Червячные передачи применяют в механизмах деления и подачи зуборезных станков, продольно-фрезерных станков, глубоко расточных станков, грузоподъемных и тяговых лебедках, талях, механизмах подъема грузов, стрел и поворота автомобильных и железнодорожных кранов, экскаваторах, лифтах, троллейбусах и других машинах.
Червяки. По форме поверхности, на которой нарезается резьба, различают – цилиндрические (рисунок 11.20, а) и глобоидные (рисунок 11.20, б) червяки. По форме профиля резьбы – с прямолинейным (рисунок 11.21, а) и криволинейным (рисунок 11.21, б) профилем в осевом сечении. Чаще применяют цилиндрические червяки. У червяков с прямолинейным профилем в осевом сечении в торцовом сечении витки очерчены архимедовой спиралью, поэтому называют архимедов червяк, который подобен ходовому винту с трапецеидальной резьбой.
Эвольвентные червяки имеют эвольвентный профиль в торцовом сечении и поэтому подобны косозубым эвольвентным колесам, у которых число зубьев равно числу заходов червяка. Основные геометрические параметры червяка: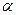 
= 20° -профильный угол (в осевом сечении для архимедовых червяков и в нормальном сечении зуба с нарезкой эвольвентного червяка); р – шаг зубьев червяка и колеса, соответствующий делительным окружностям червяка и колеса; т=
осевой модуль; z1. – число заходов червяка; 
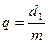– коэффициент диаметра червяка; 
– угол подъема винтовой линии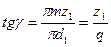 
; d1=qm – диаметр делительной окружности (здесь и далее см. рисунок 11.21); da1 = d1 + 2m – диаметр окружности выступов; dfl = d1 – 2,4m – диаметр окружности впадин; b1 – длина нарезанной части червяка, ее определяют по условию использования одновременного зацепления наибольшего числа зубьев колеса [при z1 = 1...2 b1>(11 + 0,06z2)m при z1 = 4 b1 ≥ (12,5 + 0,09z2)m].
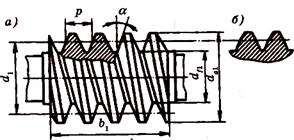
Рисунок 11.21 – Форма профиля резьбы червяка и основные геометрические параметры
По стандарту, z1 = 1; 2; 4. Рекомендуют: z1= 4 при передаточном отношении i = 8 – 15; z1 = 2 при i = 15 – 30; zг = 1 при i ≥ 30.
Значения m и q стандартизованы.
Червячные колеса. При нарезании без смещения (рисунок 11.22):
d2 = z2m – диаметр делительной окружности в главном сечении;
da2 = d2 + 2m – диаметр окружности выступов в главном сечении;
df2 = d2 – 2,4m – диаметр окружности впадин в главном сечении;
aw = 0,5(q + z2)m – межосевое расстояние.
В таблице 11.3 размеры b2 -- ширина червячного колеса и daM2 – наибольший диаметр колеса, соответствующие углу обхвата червяка колесом 2δ = 100° для силовых передач:
Таблица 11.3
| z1 | |||
| daM2 | ≤dа2+2т | ≤dаг+1,5т | ≤da2+m |
| b2 | ≤0,75da1 | ≤0,67dal |
Примечание. Число зубьев колеса из условия неподрезания принимают:
z2 = ≥ 28.
Точность изготовления. Для червячных передач стандартом предусмотрено двенадцать степеней точности. Для передач, от которых требуется высокая кинематическая точность, рекомендуют III, IV, V и VI степени точности; для силовых передач рекомендуют V, VI, VII, VIII и IX степени точности.
Рисунок 11.22 – Основные геометрические параметры червячного колеса
Передаточное отношение. В червячной передаче в отличие от зубчатой окружные скорости v1 и v2 не совпадают (см. рис. 11.23). Они направлены под углом 90° и различны по величине, относительном движении делительные цилиндры не обкатываются как у зубчатых цилиндрических и конических передачах, а скользят. При одном обороте червяка колесо повернется на угол, охватывающий число зубьев колеса, равное числу заходов червяка. Колесо сделает полный оборот при 
оборотов червяка, то есть
(11.65)
Так как z1 может быть равным 1, 2 или 4 (чего не может быть у шестерни), то в одной червячной паре можно получить большое передаточное отношение.
Скольжение в зацеплении. При движении витки червяка скользят по зубьям колеса, как в винтовой паре. Скорость скольжения vs направлена по касательной к винтовой линии червяка. Как относительная скорость она равна геометрической разности абсолютных скоростей червяка и колеса, которыми являются окружные скорости vl и v2 (см. рис. 11.19 и рис. 11.23);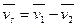 
или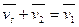 
, при этом
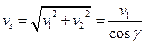
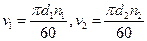
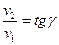
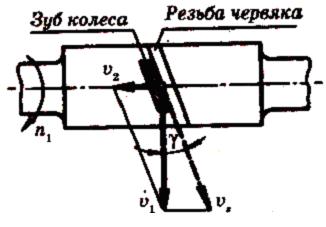
Рис. 11.23. Схема определения скорости скольжения
где – угол подъема винтовой линии червяка. Так как < 30°, то в червячной передаче v2 меньше v1 a vs больше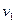 
Большое скольжение в червячных передачах служит причиной пониженного КПД, повышенного износа и склонности к заеданию.
КПД червячной передачи определяют по формуле (11.48). Различие только в определении потерь в зацеплении. По аналогии с винтовой парой К.П.Д. зацепления при ведущем червяке определяется по формуле:
(11.67)
КПД увеличивается с увеличением числа заходов червяка (увеличивается ) и с уменьшением коэффициента трения или угла трения ф. Если ведущим является колесо, то меняется направление сил и тогда получим
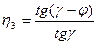(11.68)
При ≤ 
, 
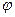3 = 0 передача движения в обратном направлении (от колеса к червяку) невозможна. Получаем самотормозящую червячную пару.
Экспериментально установлено, что коэффициент трения 
зависит от скорости скольжения. С увеличением vs снижается . Это объясняется тем, что повышение vs приводит к переходу от режимов полужидкостного трения к жидкостному трению. Значения коэффициента трения также зависят от шероховатости поверхностей трения и качества смазки.
Для предварительных расчетов, когда и vs не известны, КПД можно выбирать по средним значениям из таблицы 11.4.
Таблица 11.4
| Z1 | |||
|
| 0,7.. .0,75 | 0,75.. .0,82 | 0,87.. .0,92 |
После определения размеров передачи КПД уточняют расчетом.
Силы в зацеплении. В червячном зацеплении (см. рис. 11.24) действуют: окружная сила червяка Ft1, равная осевой силе червяка Fa2,
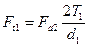(11.69)
окружная сила колеса Ft2, равная осевой силе червяка Fa1
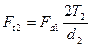(11.70)
радиальная сила
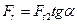(11.71)
нормальная сила
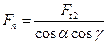(11.72)
В осевой плоскости силы Ftz и Fr являются составляющими Fn = Fncos(проекция нормальной силы на осевую плоскость). Т1 -- момент на червяке, Т2 — момент на колесе:
Т2=Т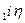
(11.73)
Основные критерии работоспособности и расчета. Червячные передачи рассчитывают по напряжениям изгиба и контактным напряжениям. Здесь чаще наблюдается износ и заедание. Это связано с большими скоростями скольжения и неблагоприятным направлением скольжения относительно линии контакта. Для предупреждения заедания применяют специальные антифрикционные пары материалов: червяк — сталь, колесо — бронза или чугун.
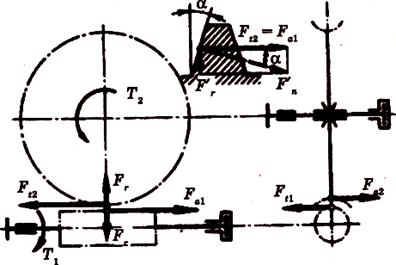
Рис. 11.24. Силы в червячном зацеплении
Интенсивность износа зависит от контактных напряжений. Основной расчет ведут по контактным напряжениям. Расчет по напряжениям изгиба выполняется как проверочный.
Расчет по контактным напряжениям. Уравнение
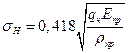(11.74)
применяют и для расчета червячных передач. Для архимедовых червяков радиус кривизны витков червяка в осевом сечении ρ1 =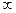 
. Тогда по формуле (11.8) с учетом уравнения (11.20) получим
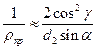(11.75)
По аналогии с косозубой передачей, удельная нагрузка червячных передач
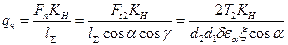(11.76)
где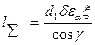 
– суммарная длина контактной линии (см. рис. 11.22); 
α= 1,8...2,2 – торцовый коэффициент перекрытия в средней плоскости червячного колеса;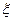 
≈ 0,75 – коэффициент, учитывающий уменьшение длины контактной линии в связи с тем, что соприкосновение обеспечивается не по полной дуге обхвата 2δ. После подстановки в формулу (11.74) получим
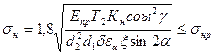(11.77)
Для проектного расчета (11.77) решают относительно 
, заменяя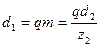 
и принимая 
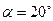, Кн=1,1, 
, 
, 
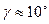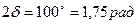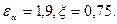При этом
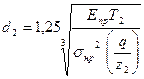(11.78)
Учитывая
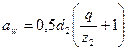(11.79)
произведем расчет по формуле (11.78) относительно межосевого расстояния
(11.80)
В формулах (11.77)…(11.80)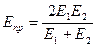 
, где Е1 и Е2 – модули упругости материалов червяка и колеса: 
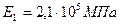– сталь; 
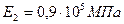– бронза, чугун. При проектном расчете отношением 
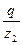, задаются. Для силовых передач принимают 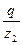= 0,22…0,4.
Расчет по напряжениям изгиба. На изгибную прочность рассчитывают только зубья колеса, так как витки червяка по материалу прочнее зубьев колеса. В расчетах червячное колесо рассматривают как косозубое. В формулу (11.32) вводят следующие поправки и упрощения.
1. По своей форме зуб червячного колеса прочнее зуба косозубого колеса (примерно на 40%). Это связано с дуговой формой зуба. Особенности формы зуба червячных колес учитывает коэффициент формы зуба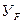 
, который выбирают по справочникам в зависимости от эквивалентного числа зубьев.
2. Червячная пара хорошо прирабатывается. Поэтому принимают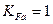 
и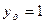 
(см. формулу (11.34)) и, далее,
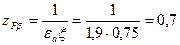
Тогда формулу (11.32) можно записать в виде
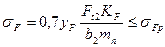(11.81)
где уF – коэффициент формы зуба, который выбирают по эквивалентному числу зубьев колеса 
; нормальный модуль тп = mcos(здесь т – осевой модуль); KF – коэффициент расчетной нагрузки.
Для червячных передач принимают Кн = KF = Kv Кβ, где Kv -- коэффициент динамической нагрузки; К
-- коэффициент концентрации нагрузки. При сравнительно высокой точности изготовления принимают Кv=1при vs < 3 м/с; Kv = 1...1,3 при vs > 3 м/с.
При постоянной внешней нагрузке Кβ =1; при переменной нагрузке Кβ = 1,05...1,2 – большие значения при малых q и больших z2.