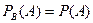Теорема сложения вероятностей.

Теоремы сложения и умножения вероятностей.

 

Как правило, для определения вероятностей событий применяются не непосредственные прямые методы, а косвенные, позволяющие по известным вероятностям одних событий определять вероятности других событий, с ними связанных. Применяя косвенные методы, мы всегда в той или иной форме пользуемся основными теоремами теории вероятностей – теоремами сложения и умножения вероятностей. Эти теоремы могут быть доказаны только для событий, сводящихся к схеме случаев. Для остальных событий они принимаются аксиоматически.

 

Вероятность суммы двух любых событий равна сумме вероятностей этих событий без вероятности их произведения:

Р(А+В)=Р(А)+Р(В)-Р(АВ)

(доказательство самостоятельно)

Следствия: 1. Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: .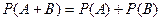

2. Сумма вероятностей событий, образующих полную группу, равна 1.

Частный случай: .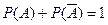

3. В случае суммы трёх и более событий проще перейти к противоположному событию: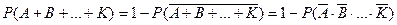

Пример: В колоде 36 карт. Объявлен козырь. Какова вероятность того, что вынутая наудачу карта будет козырем или тузом?

Решение: Пусть событие А – вынутая карта козырь, событие В – вынутая карта туз.

Тогда Р(А+В)=Р(А)+Р(В)-Р(АВ)=.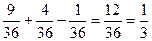

 

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет.

Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло событие В или нет.

Пример: В урне 2 белых и 1 чёрный шар. Вынимают два шара. ассматриваются события: А – появление первого белого шара, В – появление второго белого шара. Вероятность события В если известно, что первый шар возвращается в урну, равна - 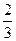, если известно, что не возвращается, становится равной 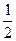. Следовательно, В зависит от А.

Вероятность события А, вычисленная при условии, что имело место другое событие В, называется условной вероятностью события А и обозначается

Условие независимости события А от события В: