Метод потенциалов

Лекция 2

Решение транспортной задачи любым способом производится на макете. Макет для применения метода потенциалов имеет следующий вид (табл. 5).

Основная часть макета выделена двойными линиями. Она содержит 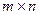клеток. Каждая клетка в этой части обозначается символом (i, j). Например, клетка, стоящая во второй строке и первом столбце, будет обозначена (2, 1). Макет содержит в себе матрицу тарифов. Назначение строки v_j и столбца u_i будет выяснено в дальнейшем.

Прежде чем приступить к изложению метода, рассмотрим некоторые предварительные понятия.

Произвольную совокупность клеток в макете называют набором. Цепью называется последовательный набор клеток, в котором каждые две соседние клетки расположены в одном ряду (строке, столбце), причем никакие три клетки в одном ряду не располагаются.

Таблица 5

Макет для метода потенциалов

Пункты назначения Пункты отправления V_j U_i	B₁	B₂	…	B_j	…	B_n	Запасы груза

A₁		с₁₁ х₁₁	с₁₂ х₁₂	…	с₁_j х₁_j	…	с₁_n х₁_n	a₁
А₂		с₂₁ х₂₁	с₂₂ х₂₂	…	с₂_j х₂_j	…	с₂_n х₂_n	a₂
…		…	…	…	…	…	…	…
А_i		с_i1 х_i1	с_i2 х_i2	…	с_ij х_ij	…	с_in х_in	a_i
…		…	…	…	…	…	…	…
А_m		с_m1 х_m1	с_m2 х_m2	…	с_mj х_mj	…	с_mn х_mn	a_m
Потребности в грузе	b₁	b₂	…	b_j	…	b_n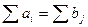

Пример цепи приведен в табл. 6. Прямые, соединяющие взятые клетки, пересеклись, но так как клетку в пересечении мы не берем, правило цепи не нарушается.

Если последняя клетка цепи расположена в одном ряду с первой, то такая замкнутая цепь называется циклом. Пунктиром цепь из табл. 6 достраивается до цикла табл. 7.

Таблица 6 Таблица 7

Цепь Цикл

Теорема 1. Пусть в макете (матрице) из m строк и n столбцов произвольно отмечено m+n клеток, причем . В этом случае всегда можно построить цикл, вершины которого лежат в отмеченных клетках (может быть не во всех).

Замечание. Числа m и n целые, и для них не всегда будет выполнено неравенство . Если одно из этих чисел — единица, это неравенство не выполняется. Например, при m = 3, n = 1 имеем 3+1 > 3•1. Однако при m = 2 и n = 2 будет 2+2 = 2•2, а при m и n, одновременно больших двух, неравенство всегда выполняется. Условие исключает случаи матриц с одной строкой или одним столбцом, в которых вообще цикла построить нельзя.

Допустимый план X(x_ij) называется ациклическим (нециклическим), если набор клеток с отличными от нуля, компонентами плана x_ij > 0 не содержит ни одного цикла.

Если в ациклическом плане X (x_ij) число положительных компонент

(остальные компоненты — нули), то элементы c_ij матрицы тарифов из набора клеток, в которых расположены x_ij > 0, будем называть базисными (Х-отмеченными).

Если же число положительных компонент плана

то к клеткам, занятым положительными x_ij, добавляем недостающие до (m + n – 1) из нулевых клеток, лишь бы присоединенные клетки вместе с уже взятыми не допускали циклов. Тарифы c_ij всех взятых клеток, равно как и сами клетки, включаются в число базисных.

Больше (m + n – 1) число компонент ациклического плана не может быть, так как уже при N = m + n по теореме 1 всегда из выбранных клеток можно построить цикл.

Теорема 2. Если для некоторого плана X = (x_ij)_mxn транспортной задачи можно подобрать систему из m + n чисел u₁, u₂, ... , u_m; v₁, v₂ , ... , v_n, удовлетворяющую следующим условиям:

(1)

для всех , а для x_ij>0

(2)

то план X будет оптимальным.

Числа u_i, v_j называются потенциалами пунктов отправления и пунктов назначения; условия (1) и (2) называют условиями потенциальности плана X.

К каждой клетке (i, j) относятся два потенциала: i-гo пункта отправления u_i и j-го пункта назначения v_j. Условия потенциальности словесно можно сформулировать так: разность потенциалов для всех без исключения клеток должна быть меньше или равна тарифу, а для базисных клеток она должна быть точно равна тарифу. План, удовлетворяющий этим условиям, называется потенциальным.

С учетом такой терминологии основную теорему можно изложить короче: если некоторый план транспортной задачи потенциален, то он оптимален и наоборот.