Числовые характеристики случайных величин.

Для решения многих практических задач вовсе не нужно знать распределение СВ, а достаточно знать лишь некоторые числа, характеризующие их распределение, так называемые числовые характеристики СВ.

1. Математическое ожидание.

Математическим ожиданием случайной величины X, называется величина

В случае ряда (n=) и несобственного интеграла предполагается, что они абсолютно сходятся, в противном случае математическое ожидание не существует.

Смысл математического ожидания состоит в следующем: если проведено большое количество опытов и в каждом из них определено значение случайной величины, то среднее арифметическое полученных значений приближенно равно математическому ожиданию, чем больше число опытов, тем «ближе» среднее наблюдаемых значений к математическому ожиданию.

Так как математическое ожидание теоретическая величина, которую можно найти без проведения опытов, то тем самым можно указать среднее значение случайной величины в большом числе опытов без проведения самих опытов.

Поэтому математическое ожидание называют также средним значением, средним ожидаемым, центром рассеивания, центром распределения.

Обозначение: M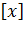, M(x), M(X), . Размерность математического ожидания совпадает с размерностью самой случайной величины.

Примеры: 1) пусть Х дсв:

0,09	0,42	0,49

M(Х)=0∙0,9+1∙0,42+2∙0,49=1,4

2) пусть Х нсв:

M()=.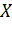

Свойства математического ожидания:

1) M(C)=C, где С - некоторая постоянная величина.

2) M(C∙X)=C∙M(X).

3) M(X+Y)=M(X)+M(Y) .

4) M(X∙Y)=M(X)∙M(Y), если Х и Y независимые случайные величины.

5) Если Y=φ(X) функция от случайной величины Х, то

 

Различные случайные величины могут иметь одно и то же математическое ожидание.

Пример:

-0,1	0,2

Х

M(Х)=0

 

Y M(Y)=0

-100

Однако характер распределения Х и Y существенно различен. Случайная величина Х принимает значения мало отличающиеся от ее математического ожидания, величина Y принимает значения значительно удаленные от ее математического ожидания. Поэтому вводится еще одна числовая характеристика для измерения степени рассеивания, разброса значений, принимаемых случайной величиной вокруг ее математического ожидания.

 

2. Дисперсия.

Центрированной случайной величиной или отклонением, называется случайная величина .

На основании свойств математического ожидания:

M(.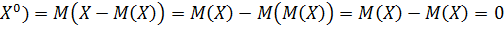

Дисперсия есть математическое ожидание квадрата отклонения:

D()=M((-M(

Используя определение математического ожидания, можно получить:

Размерность дисперсии равна квадрату размерности самой случайной величины.

Обозначение: D(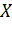), D(x), D, .

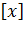Среднее квадратическое отклонение случайной величины это величина:

Размерность среднего квадратического отклонения совпадает с размерностью самой случайной величины.

Пример:

1) Пусть дсв:

0,09	0,42	0,49

M(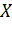)=0∙0,09+1∙0,42+2∙0,49=1,4

D(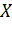)=0,09+0,42+.

2) Пусть нсв:

M()=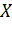

.

Свойства дисперсии:

1) D(C)=0, где С - некоторая постоянная величина.

2) D(C∙X)=.

3) (дисперсия равна математическому ожиданию квадрата случайной величины минус квадрат математического ожидания).

4) Если Х и Y независимые случайные величины, то

D(X=D(X)+D(Y).

5) Если Х и Y зависимые случайные величины, то

D(X=D(X)+D(Y)+2∙ M(.

Число M(называется корреляционным моментом случайных величин X и Y, и обозначается К(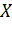, Y). Зависимые случайные величины иногда называют скоррелированными друг с другом. Коэффициентом корреляции называется число r(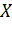, Y)=.

Замечание: обратим внимание на интерпретацию математического ожидания и дисперсии в финансовом анализе. Пусть, например, известно распределение доходности 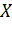некоторого актива. Тогда M(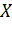) выражает среднюю (прогнозную) доходность актива, а D(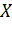) или - меру отклонения, колеблемости доходности от ожидаемого среднего значения, то есть риск данного актива.

3. Моменты случайных величин.

Пусть 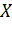случайная величина kN.

Величина M(называется начальным моментом k-го порядка. Математическое ожидание – начальный момент первого порядка.

Величину M((называют центральным моментом k-го порядка. Дисперсия – центральный момент второго порядка.

Величина M() - абсолютный момент k-го порядка.

Замечание: моменты высших порядков служат для более подробного описания распределения. Так, например, третий центральный момент M((характеризует ассиметрию распределения; четвертый центральный момент M((характеризует крутость распределения…

 

4. Мода и медиана случайной величины.

Модой (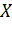) случайной величины 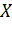называют её наиболее вероятное значение, для которого вероятность 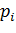или плотность вероятности f(x) достигают максимума.

Если вероятность или плотность вероятности достигают максимума не в одной, а в нескольких точках, то распределение называют полимодальным.

Медианой непрерывной случайной величиной 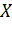называют такое её значение, для которого P(=P(

Пример: найти моду, медиану, математическое ожидание случайной величины 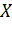, если f(x)=3при xвне указанного отрезка f(x)=0.

Из рисунка видно, что функция f(x) достигает максимума при х=1, следовательно,

, тогда , отсюда .

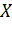M()=

M(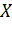)