Дифференциальное уравнение линий тока.

Получим дифференциальное уравнение линий тока. Учтем, что векторный элемент , совпадает с направлением вектора скорости , т.е. эти два вектора коллиниарны êê .

Векторное произведение двух коллиниарных векторов равно нулю.

Раскроем векторное произведение

, (3.1)

Если векторное произведение =0, то равны нулю все слагаемые уравнения (3.1). Поделим каждое из этих слагаемых на произведение фигурирующих в данном слагаемом скоростей и получим

, ,

или

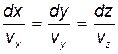- . (3.2)

Уравнение (3.2) называется уравнением линий тока

(3.3.)

Уравнение (3.3) является уравнением траектории

3.3.Гидравлические элементы потока.

	Трубка тока – совокупность линий тока, проходящих через замкнутый контур l.

 

 

 

 

Иногда говорят так, что элементарная струйка – это обтелесенная линия тока.