Уравнение Лапласа

Гармонические поля

Любое векторное поле можно представить в виде суммы потенциального и соленоидального полей (теорема Гельмгольца).

Векторное поле a называется гармоническим, если оно одновременно и потенциальное и соленоидальное, т.е. если:

(8.30)

Из условия потенциальности гармонического поля следует, что векторное поле можно представить a = gradj. Подставив это во второе уравнение, получим или

. (8.31)

Это уравнение называется уравнением Лапласа. В связи с этим гармонические поля часто называют лапласовыми. Функции j, удовлетворяющие уравнению Лапласа, называются гармоническими.

Замечание. Уравнение Лаплас впервые встретилось у Л. Эйлера (1761) и Ж. Даламбера (1761)в связи задачами гидродинамики. Однако широкую известность это уравнение получило после появления работ П. Лапласа (1782, 1799) по теории гравитационного потенциала и небесной механики.

Пример 8.4. Доказать гармоничность поля сил тяготения и поля кулоновских сил точечного заряда.

Решение. Потенциал поля тяготения (или электростатического поля) имеет вид

,

где 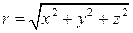, k = const. Проверим. Что эта функция гармоническая. Учитывая, что

получим

, .

Аналогично получаем

, .

Окончательно находим

.

Упражнение. Определите типы полей, изображенных на рис. 8.6.

Рис. 8.6