Циркуляция потенциального поля между двумя точками

Теорема. Циркуляция односвязного потенциального поля между двумя точками не зависит от пути, соединяющего эти точки, и равна разности значений потенциала поля в этих точках:

. (8.21)

Действительно, рассмотрим две точки A и B и два пути между ними ACB и ADB (см. рис. 8.1). Если векторное поле a потенциально, то циркуляция по контуру ACBDA будет равна нулю:

.

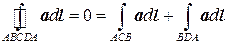Изменим направление интегрирования во втором интеграле, тогда

.

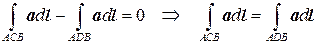Следовательно, криволинейный интеграл для потенциального поля не зависит от пути интегрирования, а зависит только от начальной и конечной точек.

Если векторное поля является потенциальным, то его можно представить в виде градиента некоторой функции (потенциала): a=gradj. Тогда справедливо равенство

, (8.22)

что легко проверяется, если расписать обе части этого равенства. Тогда

.

Замечание. Равенство (8.22) справедливо только для потенциальных полей, т.е. элемент циркуляции векторного поля (gradj dl) является полным дифференциалом некоторой функции, тогда и только тогда, когда поле является потенциальным.