Теорема Стокса

Теорема. Циркуляция дифференцируемого векторного поля a по произвольному кусочно-гладкому замкнутому контуру L равна потоку вектора rota через поверхность S, ограниченную контуром L:

(7.9)

Здесь единичный вектор n нормали к поверхности S направлен в такую сторону, чтобы обход контура L происходил в положительном, по отношению к n, направлении.

Замечание 4. Формула (7.9), только в координатной форме, впервые была получена Дж. Стоксом в 1854 г.

Доказательство. Пусть поверхность S, ограниченной кривой L, разбита на большое число малых участков Ds_i, ограниченных линиями Dl_i. Тогда, в соответствии с определением ротора, можно написать , где означает значение ротора в какой-либо точке на поверхности Ds_i. Просуммируем обе части этого равенства по всем участкам поверхности:

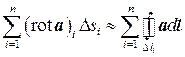. (7.10)

Левая часть полученного равенства при n®¥ (Ds_i®0) можно выразить в виде поверхностного интеграла 2-го рода:

.

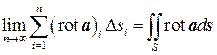Сумму в правой части (7.10) преобразуем следующим образом. Все внутренние участки соприкасаются друг с другом. Тогда все криволинейные интегралы по линиям соприкосновения будут входить в указанную сумму два раза, но в разных направлениях. В результате, в сумме эти интегралы дадут нуль. Следовательно, останется лишь сумма интегралов по внешней линии L:

.

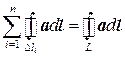Таким образом, мы получаем формулу Стокса.

Пример 7.6. Вычислить циркуляцию векторного поля a=x²y³i+j+zk по окружности L: x²+y²=R², z=0.

Решение. Поскольку rota=–3x²y²k (см. пример 7.4), то по теореме Стокса получаем

.

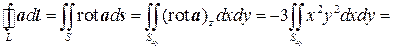
Такой же получится ответ, если непосредственно вычислить криволинейный интеграл 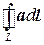.