Криволинейные интегралы 2-го рода

ЦИРКУЛЯЦИЯ И РОТОР ВЕКТОРНОГО ПОЛЯ

ЛЕКЦИЯ 8

Рис. Ротационный компрессор

 

Наряду с этим ротационные компрессоры имеют следующие недостатки:

- меньший КПД, чем у поршневых

машин;

- большая точность изготовления и более сложная технология;

- ограниченное конечное давление.

Вопросы для самоконтроля

1. Область применения компрессорного оборудования в нефтя­ной промышленности.

2. Принцип действия поршневого компрессора.

3. Условия сжатия газа в поршневых компрессорах. Политропный процесс.

4. Идеальная индикаторная диаграмма цикла поршневого комп­рессора.

5. Работа на сжатие единицы массы газа в компрессоре.

6. От чего зависит температура в конце процесса сжатия в одной

7. ступени?

8. Производительность поршневых компрессоров.

9. Объемный коэффициент подачи поршневого компрессора.

10. Что такое степень сжатия?

11. Принцип получения высоких давлений в поршневых компрессорах.

12. Многоступенчатые поршневые компрессоры.

13. Индикаторная диаграмма поршневого компрессора.

14. Охлаждение сжимаемого газа между ступенями.

15. Принцип расчета системы охлаждения.

16. Конструкция межступенчатых теплообменников.

17. Определение полезной мощности компрессора.

18. Определение эффективной мощности компрессора, КПД ком­прессора.

19. Принцип действия винтового компрессора.

20. Чем отличаются винтовые компрессоры «мокрого» и «cyxoгo» сжатия?

21. Классификация поршневых компрессоров.

22. Конструкция клапанов поршневых компрессоров.

23. Что такое дифференциальный поршень?

24. Конструкция уплотнения штоков.

25. Циркуляционная система смазки поршневых компрессоров.

26. Лубрикаторная система смазки компрессора.

27. Принцип действия турбокомпрессора.

28. Что такое помпажная зона центробежного компрессора?

29. Конструкция центробежного компрессорного агрегата.

30. Уплотнения в центробежных компрессорах.

31. Чем образована рабочая камера ротационного компрессора?

32. Регулирование работы поршневого компрессора.

33. Влияние «мертвого» пространства на работу компрессора.

34. Эксплуатация поршневых компрессоров.

35. Эксплуатация винтовых компрессоров.

36. Эксплуатация центробежных компрессоров.

37. Неисправности поршневых компрессоров.

 

Циркуляция и ротор векторного поля. Криволинейные интегралы 2-го рода. Ротор векторного поля. Теорема Стокса. Формула Грина.

 

Пусть в некоторой области задано векторное поле

a = a_xi + a_yj + a_zk

и какая-либо кривая L. Разобьем кривую каким-либо способом на элементарные участки Dl_i. На каждом участке возьмем произвольную точку P_i и составим интегральную сумму:

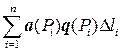, (7.1)

где q(P_i) – единичный вектор, совпадающий по направлению с касательной, проведенной к кривой L в точке P_i. Если существует предел такой суммы при Dl_i®0, то этот предел называется криволинейным интегралом 2-го рода и обозначается символом

, или ,

где dl=qdl.

Поскольку единичный направляющий вектор q имеет своими координатами направляющиеся косинусы q={cosa, cosb, cosg}, то

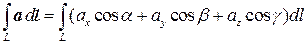. (7.2)

Этот интеграл представляет собой не что иное, как криволинейный интеграл
1-го рода. Таким образом, вычисление криволинейных интегралов 2-го рода можно свести к вычислению криволинейных интегралов 1-го рода.

В отличие от криволинейных интегралов 1-го рода криволинейные интегралы 2-го рода зависят от направления, по которому совершается интегрирование вдоль дуги кривой AB:

.

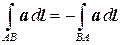Криволинейные интегралы 2-го рода (по аналогии с поверхностными интегралами 2-го рода) можно записать в виде

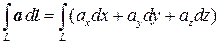, (7.3)

где учтено, что cosadl=dx, cosbdl=dy, cosgdl=dz. Отметим, что здесь уже не обязательно писать знак ± перед интегралами, как мы это делали в случае поверхностных интегралов 2-го рода. Это связано с тем, что в дальнейшем это будет учтено при проецировании кривой L на координатные оси.

Замечание 1. Криволинейные интегралы 2-го рода (в соответствии с формулой (7.3)) часто записывают в виде

,

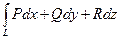где P, Q, R – какие-то функции, заданные на кривой L. В связи с этим криволинейные интегралы 2-го рода иногда называют криволинейными интегралами по координатам, а криволинейные интегралы 1-го рода иногда – криволинейными интегралами по длине.

Криволинейный интеграл 2-го рода легко сводится к определенному интегралу, если уравнение кривой L задано параметрически: x=x(t), y=y(t), z=z(t). Если при движении по кривой L от точки A до точки B параметр t меняется от t₁ до t₂, то криволинейный интеграл 2-го рода вычисляется по следующей формуле:

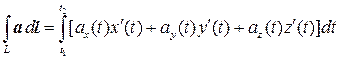. (7.4)

Пример 7.1. Вычислить работу векторного поля

a = 2x²yi – xy²j

от начала координат O до точки A(1;1), если движение происходит вдоль:
а) отрезка прямой [OA]; б) дуги параболы ; в) ломаной OBA, где B(1;0) (см. рис. 7.1).

Решение. а) Уравнение прямой OA имеет вид y=x. Пусть x=t, тогда уравнение прямой в параметрическом виде примет вид:

x=t, y=t,

причем при движении от A до B параметр t будет меняться от 0 до 1. Тогда совершенная работа будет равна

.

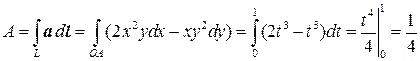б) Пусть x=t², y=t, тогда

x=t², y=t, 0£t£1.

Далее получаем

.

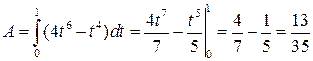в) Уравнение прямой (OB) имеет вид y=0 (0£x£1); уравнение прямой (BA) имеет вид x=1 (0£y£1). Тогда

, .

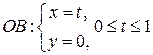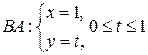В результате, получаем,

.

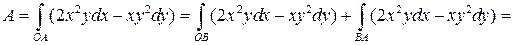
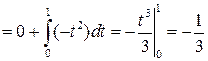Замечание 2. Если в случае двухмерных полей уравнение линии описывается уравнением y=y(x), а переменная x изменяется от a до b, то криволинейный интеграл 2-го будет вычисляться по формуле:

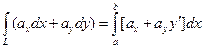. (7.5)

Предыдущий пример можно было бы решить и при помощи этой формулы, не вводя параметр t.

Как уже отмечалось, особое значение в математике и ее приложениях играют криволинейные интегралы по замкнутой кривой (контуру). Такие интегралы называются циркуляциями и обозначаются

.

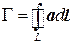Пример 7.2. Вычислить циркуляцию поля скоростей вращающегося твердого тела:

v = –wyi+wxj

вдоль окружности, лежащей в плоскости xOy:

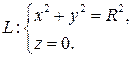
Решение. Запишем уравнение окружности в параметрическом виде

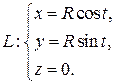
Если движение по окружности не указано, то оно должно происходить против часовой стрелки. Тогда параметр будет изменяться от 0 до 2p. В результате, получим

,

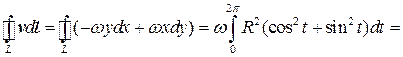
где S – площадь круга. Этот результат является частным случаем более общей теоремы, утверждающей, что циркуляция в поле скоростей вращающегося твердого тела не зависит от формы контура и находится в прямой зависимости от площади, ограниченной этим контуром.

Пример 7.3. Вычислить циркуляцию магнитного поля, образуемого прямолинейным бесконечным проводником с постоянным током I:

.

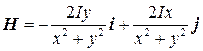вдоль окружности, лежащей в плоскости xOy:

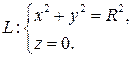
Решение. Выражение для магнитного поля получается из закона Био-Савара-Лапласа, если ось Oz направить вдоль проводника. Записывая уравнение окружности в параметрической форме, как в предыдущем примере, получим

.

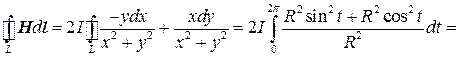
Этот результат также является частным случаем более общей теоремы, утверждающей, что циркуляция магнитного поля проводника с током не зависит от выбора контура обхода вокруг проводника, а зависит от силы тока в проводнике.