Векторное поле
Векторным полем называется часть пространства, каждой точке которого поставлен в соответствие определённый вектор.
Примеры векторных полей: 1) поле скоростей текущей жидкости;
2) силовые поля: электрическое, магнитное, гравитационное.
Векторное поле считается заданным, если в каждой его точке М определена векторная функция 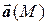 . Если векторное поле отнесено к декартовой системе координат, то векторную функцию можно записать в виде:
. Если векторное поле отнесено к декартовой системе координат, то векторную функцию можно записать в виде:
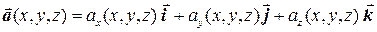 .
.
Простейшей геометрической характеристикой векторного поля являются векторные линии.
Векторные линии – это линии, в каждой точке которой касательная имеет направление соответствующего ей вектора.
Примеры векторных линий: 1) если рассматривается поле скоростей текущей жидкости, то векторные линии суть линии тока этой жидкости, т.е. траектории движения частиц жидкости; 2) для геометрического представления магнитного поля используются магнитные силовые линии (для экспериментального изображения магнитных силовых линий используют металлические опилки, насыпанные на лист бумаги, в магнитном поле эти опилки выстраиваются вдоль силовых линий).
Замечание. Наряду с понятием векторной линией, часто используется также и понятие векторной трубки. Векторной трубкой называется поверхность, образованная векторными линиями, проходящими через точки некоторой лежащей в поле замкнутой кривой, не совпадающей (даже частично) с какой-либо векторной линией.
В вопросах, связанных с изучением полей важную роль играет задача о нахождении векторной линии поля 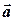 , проходящей через заданную точку M. Пусть уравнение векторной линии имеет вид
, проходящей через заданную точку M. Пусть уравнение векторной линии имеет вид
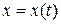 ,
, 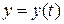 ,
, 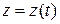
или в векторной форме
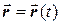 .
.
По условию в каждой точке этой линии вектор поля 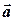 направлен по касательной к ней. Из геометрического смысла производной известно, что производная любой функции определяет направление касательной к этой функции. Поэтому, производная
направлен по касательной к ней. Из геометрического смысла производной известно, что производная любой функции определяет направление касательной к этой функции. Поэтому, производная  направлена по касательной к векторной линии. Следовательно, векторы
направлена по касательной к векторной линии. Следовательно, векторы 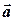 и
и  – коллинеарны. Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны. В результате получаем
– коллинеарны. Два вектора коллинеарны тогда и только тогда, когда их координаты пропорциональны. В результате получаем
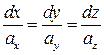 (1.1)
(1.1)
Это есть система дифференциальных уравнений для нахождения уравнений векторных линий.
Пример 1.2. Найти уравнение векторных линий векторного поля
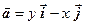 .
.
Решение. Для двухмерных полей система дифференциальных уравнений векторных линий принимает вид


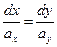
В данном случае 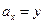 ;
; 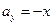 . Поэтому
. Поэтому
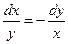
Разделяя переменные и интегрируя, получим
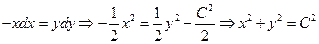 .
.
Таким образом, векторные линии представляют собой совокупность окружностей (см. рис. 1.2).