Изобразить схему замещения 3-фазного источника в случае соединения его фаз “звездой”. Привести векторную топографическую диаграмму напряжений такого источника.

Ответ: При соединение фаз обмотки генератора (или трансформатора) звездой их концы X, Y и Z соединяют в одну общую точку N, называемую нейтральной точкой (или нейтралью) (рис. 3.6). Концы фаз приемников (Z_a, Z_b, Z_c) также соединяют в одну точку n. Такое соединение называется соединение звезда.

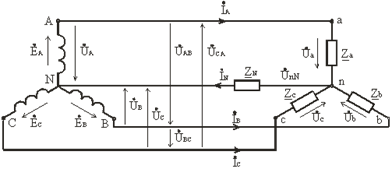Рис. 3.6

Провода A−a, B−b и C−c, соединяющие начала фаз генератора и приемника, называются линейными, провод N−n, соединяющий точкуN генератора с точкой n приемника, – нейтральным. Трехфазная цепь с нейтральным проводом будет четырехпроводной, без нейтрального провода – трехпроводной. В трехфазных цепях различают фазные и линейные напряжения. Фазное напряжение U_Ф – напряжение между началом и концом фазы или между линейным проводом и нейтралью (U_A, U_B, U_C у источника; U_a, U_b, U_c у приемника). Если сопротивлением проводов можно пренебречь, то фазное напряжение в приемнике считают таким же, как и в источнике. (U_A=U_a, U_B=U_b, U_C=U_c). За условно положительные направления фазных напряжений принимают направления от начала к концу фаз. Линейное напряжение (U_Л) – напряжение между линейными проводами или между одноименными выводами разных фаз (U_AB, U_BC, U_CA). Условно положительные направления линейных напряжений приняты от точек, соответствующих первому индексу, к точкам соответствующим второму индексу (рис. 3.6).

По аналогии с фазными и линейными напряжениями различают также фазные и линейные токи: 1)Фазные (I_Ф) – это токи в фазах генератора и приемников. 2)Линейные (I_Л) – токи в линейных проводах. При соединении в звезду фазные и линейные токи равны: I_Ф=I_Л. (3.5)

Ток, протекающий в нейтральном проводе, обозначают I_N. По первому закону Кирхгофа для нейтральной точки n (N) имеем в комплексной форме: İ_N=İ_A+İ_B+İ_C. (3.6)

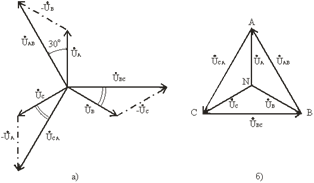Рис. 3.7

В соответствии с выбранными условными положительными направлениями фазных и линейных напряжений можно записать уравнения по второму закону Кирхгофа. Ú_AB=Ú_A−Ú_B; Ú_BC=Ú_B−Ú_C; Ú_CA=Ú_C−Ú_A. (3.7). Согласно этим выражениям на рис. 3.7а построена векторная диаграмма, из которой видно, что при симметричной системе фазных напряжений система линейных напряжений тоже симметрична: U_AB, U_BC, U_CA равны по величине и сдвинуты по фазе относительно друг друга на 120° (общее обозначение U_Л), и опережают, соответственно, векторы фазных напряжений U_A, U_B, U_C, (U_Ф) на угол 30°. Действующие значения линейных напряжений можно определить графи-чески по векторной диаграмме или по формуле (3.8), которая следует из треугольника, образованного векторами двух фазных и одного линейного напряжений: U_Л=2U_Фcos30°или U_Л= U_Ф. (3.8) Предусмотренные ГОСТом линейные и фазные напряжения для цепей низкого напряжения связаны между собой соотношениями:

U_Л=660В;U_Ф=380В;
U_Л=380В;U_Ф=220В;
U_Л=220В;U_Ф=127В.

Векторную диаграмму удобно выполнить топографической (рис. 3.7б), тогда каждой точке цепи соответствует определенная точка на диаграмме. Вектор, проведенный между двумя точками топографической диаграммы, выражает по величине и фазе напряжения между одноименными точками цепи.