ТЕРМОДИНАМИКА РЕАЛЬНЫХ РАСТВОРОВ

В настоящее время рационального математического описания термодинамики реальных растворов нет. Напомним, что Льюис и Рендал для характеристики термодинамических свойств реальных газовых растворов предложили использовать термодинамические уравнения для идеальных систем, заменив в них парциальное давление го компонента на дополнительную термодинамическую величину – парциальную фугитивность (или летучесть):

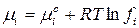, (101)

Для реальных жидких растворов действительную концентрацию в (100) заменяют термодинамической активностью :

, (103)

Известно, что активность связана с концентрацией соотношением

. (105)

Установим физический смысл коэффициента активности . С учетом (105) представим уравнение для химического потенциала (103) в виде:

, (140)

где – химический потенциал го компонента в идеальном растворе.

Преобразуем (140)

.

Физический смысл – парциальная мольная термодинамическая работа переноса 1 моль го компонента из данного реального раствора в идеальный раствор.

.

Таким образом, коэффициент активности выражает отклонение термодинамических свойств компонента в реальном растворе от термодинамических свойств этого компонента в идеальном растворе.

Причины, вызывающие отклонение от 1 могут быть как физической, так и химической природы. В основном причины делят на 2 группы:

1. изменение концентрации растворенного вещества в связи с образованием ассоциатов, сольватов и др. соединений, приводящих к изменению числа частиц в растворе;

2. изменение энергии растворенных частиц вследствие их взаимодействия друг с другом и молекулами растворителя.

Получим уравнение Гиббса – Дюгема для реального раствора для этого подставим в уравнение (137) значение из (103), получим:

.

С учетом (105), имеем:

.

Таким образом, учитывая (139), получаем:

. (141)

Уравнение (141) – уравнение Гиббса – Дюгема, характеризующее условие термодинамического равновесия в реальном растворе.

Уравнение (141) лежит в основе любой современной теории реальных растворов. Устанавливает взаимосвязь между коэффициентами активности компонентов в растворе. Например, для бинарной системы:

;

().

Проинтегрируем уравнение в определенных пределах:

.

В результате, с учетом того, что при – и , имеем:

.

Уравнение позволяет рассчитать коэффициент активности второго компонента, если известна зависимость коэффициента активности первого компонента от состава раствора.