ВЕРОЯТНОСТИ

ВЗАИМОСВЯЗЬ ЭНТРОПИИ И ТЕРМОДИНАМИЧЕСКОЙ

В классической термодинамике состояние термодинамических систем описывается с помощью небольшого числа макроскопических параметров (, , , 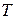), доступных непосредственному измерению. Указанные параметры характеризуют макроскопическое состояние системы. Так как система состоит из микрочастиц, то макроскопические параметры обладают статистической природой и характеризуют средние свойства большого числа микрочастиц.

В статистической термодинамике микросостояние термодинамических систем характеризуют микроскопическими параметрами – координатами молекул (, , ), определяющими их положение в пространстве, и импульсами движения молекул , характеризующими энергию их движения.

Одно и тоже макросостояние системы может быть реализовано большим числом различных микросостояний.

Число микросостояний, реализующих данное макросостояние системы, Больцман назвал термодинамической вероятностью . Чем больше , тем вероятнее пребывание системы в данном состоянии.

В статистической термодинамике предполагают, что процесс, приближающий систему к состоянию равновесия, соответствует переходу от менее вероятного состояния к более вероятному. Процесс, удаляющий систему от состояния равновесия, с точки зрения статистической термодинамики не является невозможным, просто он менее вероятен.

Таким образом, самопроизвольные процессы в изолированных системах характеризуются увеличением, как ее энтропии, так и термодинамической вероятности системы. Связь между энтропией и термодинамической вероятностью выражается уравнением Больцмана:

, (67)

где – постоянная Больцмана.

Уравнение Больцмана лежит в основе современной статистической термодинамики, связывает макро- и микропараметры системы и позволяет понять свойства энтропии как функции состояния.

При абсолютном нуле температур в системе абсолютный порядок () и энтропия . При нагревании системы возникает тепловое движение, упорядоченность в системе уменьшается, энтропия возрастает. При смешивании упорядоченность в системе может, как увеличиваться, так и увеличиваться. Таким образом, энтропия – мера беспорядка в системе.