ХИМИЧЕСКИХ РЕАКЦИЙ И ДРУГИХ ПРОЦЕССОВ

ВЛИЯНИЕ ТЕМПЕРАТУРЫ НА ТЕПЛОВЫЕ ЭФФЕКТЫ

ЛЕКЦИЯ 3

Температура оказывает большое влияние на тепловой эффект химических реакций. Количественно охарактеризуем это влияние.

а.) Рассмотрим процесс, протекающий при . Пусть энтальпия исходных веществ, участвующих в данном процессе, будет , а энтальпия веществ в конечном состоянии . Если в системе протекает реакция:

,

то, с учетом (24), изобарная теплоемкость системы в исходном состоянии:

, (37)

для продуктов реакции:

. (38)

Вычтем почленно уравнение (38) из (37), получим:

, (39)

где – разность между суммами.

б.)

Аналогично для процесса, протекающего при постоянном объеме изохорная теплоемкость системы для исходных веществ и продуктов реакции:

,

.

Следовательно,

, (40)

где .

Уравнения (39) и (40) дифференциальная форма записи закона Кирхгоффа: температурный коэффициент теплового эффекта химической реакции (термодинамического процесса), протекающей при или , равен разности сумм мольных теплоемкостей продуктов реакции и исходных веществ с учетом стехиометрических коэффициентов.

Температурный коэффициент – это производная, которая показывает на сколько изменяется величина (или ) при изменении температуры на 1 град.

В дальнейшем ограничимся рассмотрением только процессов, протекающих при , т.к. при все аналогично.

В уравнении (39) разделим переменные и проинтегрируем его в пределах от 0 до 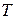, получим:

– интегральная форма записи закона Кирхгоффа.

где , – тепловой эффект процесса при температуре 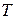и при абсолютном нуле температуры.

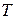Для расчета по этому уравнению теплового эффекта процесса при любой температуре необходимо знать зависимость в интервале от 0 до и . можно определить, имея набор экспериментальных данных, методами статистической термодинамики. Но получить такие данные не возможно. Т.е. данное уравнение имеет скорее теоретическое, чем практическое значение.

Гораздо удобнее с практической точки зрения провести интегрирование уравнения (39) в определенных пределах от 298 до 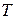. В результате получим:

, (41)

где – тепловой эффект процесса при стандартных условиях. Рассчитывается методами статистической термодинамики на основании экспериментальных данных. Значения приведены в справочнике.

Зависимость теплоемкости веществ в интервале температур от 298 до 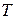чаще всего выражается экспериментальным уравнением вида:

, (31)

Тогда для реакции (процесса):

,

где ;

и т.д.

Пример: для реакции

;

и. т.д.

После подстановки значения в уравнение (41) и его интегрирования, получим:

. (42)

Уравнение (42) позволяет производить расчет теплового эффекта процесса при любой температуре.

На практике можно встретиться со случаем, когда в интервале температур от 298 до 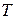одно из реагирующих веществ изменяет свое агрегатное состояние, т.е. имеет место фазовый переход (ф.п.). В этом случае интервал интегрирования разбивается на 2 части: от 298 до и от до 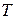. Тогда с учетом величины теплового эффекта фазового перехода уравнение (41) перепишется:

.

Если несколько веществ изменяют агрегатное состояние, то температурный интервал разбивается на соответствующее число интервалов и уравнение (41) аналогично преобразуется.