ТЕПЛОЕМКОСТЬ

Теплоемкость – это количество теплоты, которое необходимо сообщить системе для увеличения ее температуры на 1 (К) при отсутствии полезной работы и постоянстве соответствующих параметров.

Если в качестве системы мы берем индивидуальное вещество, то общая теплоемкость системы равняется теплоемкости 1 моль вещества () умноженное на число моль ().

. (16 )

Теплоемкость может быть удельная и молярная.

Удельная теплоемкость – это количество теплоты, необходимое для нагревания единицы массы вещества на 1 град (интенсивная величина).

Молярная теплоемкость – это количество теплоты, необходимое для нагревания одного моль вещества на 1 град.

Различают истинную и среднюю теплоемкость.

В технике обычно используют понятие средней теплоемкости.

Средняя– это теплоемкость для определенного интервала температур.

Если системе, содержащей количество вещества или массой , сообщили количество теплоты , а температура системы повысилась от до , то можно рассчитать среднюю удельную или молярную теплоемкость:

, . (17)

, . (18)

Истинная молярная теплоемкость– это отношение бесконечно малого количества теплоты, сообщенной 1 моль вещества при определенной температуре, к приращению температуры, которое при этом наблюдается.

. (19)

Согласно уравнению (19), теплоемкость, как и теплота, не является функцией состояния. При постоянном давлении или объеме, согласно уравнениям (11) и (12), теплота, а, следовательно, и теплоемкость приобретают свойства функции состояния, то есть становятся характеристическими функциями системы. Таким образом, получаем изохорную и изобарную теплоемкости.

Изохорная теплоемкость – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1 , если процесс происходит при .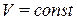

. (20)

Изобарная теплоемкость – количество теплоты, которое необходимо сообщить системе, чтобы повысить температуру на 1 при .

. (21)

Теплоемкость зависит не только от температуры, но и от объема системы, поскольку между частицами существуют силы взаимодействия, которые изменяются при изменении расстояния между ними, поэтому в уравнениях (20) и (21) используют частные производные.

Энтальпия идеального газа, как и его внутренняя энергия, является функцией только температуры:

,

а в соответствии с уравнением Менделеева–Клапейрона , тогда

. (22)

Поэтому для идеального газа в уравнениях (20), (21) частные производные можно заменить на полные дифференциалы:

. (23)

. (24)

Из совместного решения уравнений (23) и (24) с учетом (22), получим уравнение взаимосвязи между и для идеального газа.

. (25)

Разделив переменные в уравнениях (23) и (24), можно рассчитать изменение внутренней энергии и энтальпии при нагревании 1 моль идеального газа от температуры до

. (26)

. (27)

Если в указанном интервале температур теплоемкость можно считать постоянной, то в результате интегрирования получаем:

. (28)

. (29)

Установим взаимосвязь между средней и истинной теплоемкостью. Изменение энтропии с одной стороны выражается уравнением (27), с другой –

.

Приравняв правые части уравнений и выразив среднюю теплоемкость, имеем:

. (30)

Аналогичное выражение можно получить для средней изохорной теплоемкости.

Теплоемкость большинства твердых, жидких и газообразных веществ повышается с ростом температуры. Зависимость теплоемкости твердых, жидких и газообразных веществ от температуры выражается эмпирическим уравнением вида:

. (31)

где а, b, c и – эмпирические коэффициенты, вычисленные на основе экспериментальных данных о , причем коэффициент относится к органическим веществам, а – к неорганическим. Значения коэффициентов для различных веществ приведены в справочнике и применимы только для указанного интервала температур.

Теплоемкость идеального газа не зависит от температуры. Согласно молекулярно-кинетической теории теплоемкость, приходящаяся на одну степень свободы, равна (степень свободы – число независимых видов движения на которые можно разложить сложное движение молекулы). Для одноатомной молекулы характерно поступательное движение, которое можно разложить на три составляющие в соответствии с тремя взаимно перпендикулярными направлениями по трем осям. Поэтому изохорная теплоемкость одноатомного идеального газа равна

. (32)

Тогда изобарная теплоемкость одноатомного идеального газа согласно (25) определится по уравнению

. (33)

Двухатомные молекулы идеального газа помимо трех степеней свободы поступательного движения имеют и 2 степени свободы вращательного движения. Следовательно:

, .