НЕКОТОРЫХ ТЕРМОДИНАМИЧЕСКИХ ПРОЦЕССОВ

ПРИМЕНЕНИЕ I ЗАКОНА ТЕРМОДИНАМИКИ К АНАЛИЗУ

Рассмотрим в качестве примера систему, в которой протекает какой-либо процесс, единственным результатом которого является работа расширения.

Запишем уравнение I закона термодинамики

. (7)

а.) Применим уравнение (7) к анализу изохорного процесса.

Изохорным называют процесс, который протекает при постоянном объеме .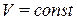

,

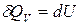после интегрирования получим:

. (11)

Из полученного результата следуют два вывода:

1. в изохорном процессе изменение внутренней энергии численно равно тепловому эффекту этого процесса;

2. тепловой эффект изохорного процесса не зависит от пути его протекания, а определяется только начальным и конечным состоянием системы. То есть в частном случае обладает свойствами полного дифференциала.

Если процесс изохорный, то работа расширения равна нулю.

б.) Изобарный процесс: 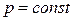. Уравнение (7) запишется в виде:

.

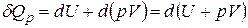Справа полный дифференциал, следовательно, можно записать:

.

Проинтегрируем:

. (12)

Из соотношения (12) следуют три вывода:

1. функция обладает всеми свойствами термодинамической функции состояния. называют энтальпией;

2. изменение энтальпии в изобарном процессе численно равно тепловому эффекту этого процесса;

3. тепловой эффект изобарного процесса не зависит от пути его протекания, а определяется только исходным и конечным состояниями системы.

Для изобарного процесса работа расширения – полный дифференциал:

.

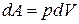После интегрирования:

. (13)

Если изобарный процесс совершается в идеальном газе и сопровождается изменением числа моль, то в соответствии с уравнением Менделеева – Клапейрона:

; ,

тогда

.

Для изобарно-изотермического процесса (все процессы, происходящие в природе, и часто встречаются в технике) :

,

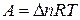где .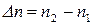

в.) Изотермический процесс .

Рассмотрим изотермический процесс, протекающий в идеальном газе, запишем уравнение I закона термодинамики (7) в виде:

.

Так как газ идеальный, а , то , тогда

. (14)

Для работы расширения будем иметь:

,

Следовательно, ,

так как в соответствии с уравнением Менделеева – Клапейрона .