ФУНКЦИЯ СОСТОЯНИЯ СИСТЕМЫ
ВНУТРЕННЯЯ ЭНЕРГИЯ КАК ТЕРМОДИНАМИЧЕСКАЯ
Докажем, что внутренняя энергия обладает всеми свойствами термодинамической функции состояния системы:
1. внутренняя энергия – функция аддитивная по определению (см. уравнение (2));
2. докажем, что изменение внутренней энергии определяется только исходным и конечным состояниями системы и не зависит от пути перехода из исходного в конечное состояние.
Для этого рассмотрим какую-либо термодинамическую систему, состояние которой характеризуется двумя параметрами, например  и
и 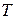 .
.
В этом случае любая точка системы отвечает определенному состоянию системы. Пусть исходное состояние характеризуется точкой 1, а конечное – точкой т. 2. Осуществим переход из точки т. 1 в т. 2 двумя различными путями.
 Обозначим через
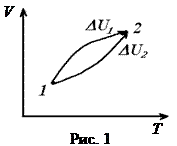
Обозначим через 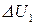 изменение внутренней энергии при переходе из т. 1 в т. 2 первым путем, а через
изменение внутренней энергии при переходе из т. 1 в т. 2 первым путем, а через  – вторым путем (рис. 1). Необходимо доказать, что всегда
– вторым путем (рис. 1). Необходимо доказать, что всегда  . Доказательство будем вести от противного.
. Доказательство будем вести от противного.
 1. Предположим, что
1. Предположим, что  . Для определенности положим, что
. Для определенности положим, что 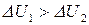 . Осуществим теперь между точками 1 и 2 циклический процесс. Из точки 1 в 2 перейдем прямым путем, а вернемся обратным (рис. 2).
. Осуществим теперь между точками 1 и 2 циклический процесс. Из точки 1 в 2 перейдем прямым путем, а вернемся обратным (рис. 2).
Получаем, что в результате осуществления циклического процесса мы получили выигрыш энергии  .
.
 Заметим, что выигрыш в энергии получен только за счет внутренней энергии. Тогда, осуществляя данный циклический процесс сколь угодно большое число раз, мы можем получить сколь угодно большой выигрыш в энергии, что равносильно созданию вечного двигателя I рода. Но это не возможно, так как противоречит I закону термодинамики. Значит наше предположение, что
Заметим, что выигрыш в энергии получен только за счет внутренней энергии. Тогда, осуществляя данный циклический процесс сколь угодно большое число раз, мы можем получить сколь угодно большой выигрыш в энергии, что равносильно созданию вечного двигателя I рода. Но это не возможно, так как противоречит I закону термодинамики. Значит наше предположение, что 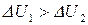 неверно.
неверно.
2. Предположим теперь, что 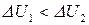 . Тогда между точкой 1 и 2 осуществим циклический процесс в обратном направлении. Из т. 1 в т. 2 перейдем прямым путем, а из точки 2 в 1 обратным (рис. 3). Получим выигрыш в энергии
. Тогда между точкой 1 и 2 осуществим циклический процесс в обратном направлении. Из т. 1 в т. 2 перейдем прямым путем, а из точки 2 в 1 обратным (рис. 3). Получим выигрыш в энергии  , но это не возможно, так как противоречит I закону термодинамики. Следовательно, это предположение так же не верно и во всех случаях
, но это не возможно, так как противоречит I закону термодинамики. Следовательно, это предположение так же не верно и во всех случаях  .
.
Вывод: таким образом, внутренняя энергия является термодинамической функцией состояния системы, а любое бесконечно малое приращение этой функции обладает свойствами полного дифференциала  .
.