Автокорреляция в остатках. Критерий Дарбина-Уотсона
Рис. 4.7.
Таблица 4.10
Таблица 4.9
Таблица 4.8
Таблица 4.7
Таблица 4.5
№ квартала,

| Количество правонарушений,

| Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| – | – | – | – | ||
| 657,5 | – | – | |||
| 655,25 | 213,75 | ||||
| 665,5 | 349,5 | ||||
| 708,75 | 693,75 | -336,75 | |||
| 709,375 | -238,375 | ||||
| 718,25 | 714,125 | 277,875 | |||
| 689,25 | 703,75 | 316,25 | |||
| 689,25 | 689,25 | -299,25 | |||
| 660,5 | 674,875 | -319,875 | |||
| 678,25 | 669,375 | 322,625 | |||
| 690,625 | 214,375 | ||||
| -233 | |||||
| 690,5 | 687,75 | -233,75 | |||
| – | – | – | – | ||
| – | – | – | – |
Шаг 2. Найдем оценки сезонной компоненты как разность между фактическими уровнями ряда и центрированными скользящими средними (гр. 6 табл. 4.5). Используем эти оценки для расчета значений сезонной компоненты 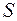 (табл. 4.6). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты
(табл. 4.6). Для этого найдем средние за каждый квартал (по всем годам) оценки сезонной компоненты  . В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
. В моделях с сезонной компонентой обычно предполагается, что сезонные воздействия за период взаимопогашаются. В аддитивной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна нулю.
Таблица 4.6
| Показатели | Год | № квартала, 
| |||
| I | II | III | IV | ||
| – | – | 213,75 | 349,5 | ||
| -336,75 | -238,375 | 277,875 | 316,25 | ||
| -299,25 | -319,875 | 322,625 | 214,375 | ||
| -233 | -233,75 | – | – | ||
Всего за  -й квартал -й квартал
| -869 | -792 | 814,25 | 880,125 | |
Средняя оценка сезонной компоненты для  -го квартала, -го квартала, 
| -289,667 | -264 | 271,417 | 293,375 | |
Скорректированная сезонная компонента, 
| -292,448 | -266,781 | 268,636 | 290,593 |
Для данной модели имеем:
 .
.
Корректирующий коэффициент:  .
.
Рассчитываем скорректированные значения сезонной компоненты ( ) и заносим полученные данные в таблицу 4.6.
) и заносим полученные данные в таблицу 4.6.
Проверим равенство нулю суммы значений сезонной компоненты:
 .
.
Шаг 3. Исключим влияние сезонной компоненты, вычитая ее значение из каждого уровня исходного временного ряда. Получим величины  (гр. 4 табл. 4.7). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.
(гр. 4 табл. 4.7). Эти значения рассчитываются за каждый момент времени и содержат только тенденцию и случайную компоненту.

| 
| 
| 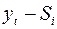
| 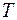
| 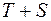
| 
| 
|
| -292,448 | 667,448 | 672,700 | 380,252 | -5,252 | 27,584 | ||
| -266,781 | 637,781 | 673,624 | 406,843 | -35,843 | 1284,721 | ||
| 268,636 | 600,364 | 674,547 | 943,183 | -74,183 | 5503,117 | ||
| 290,593 | 724,407 | 675,470 | 966,063 | 48,937 | 2394,830 | ||
| -292,448 | 649,448 | 676,394 | 383,946 | -26,946 | 726,087 | ||
| -266,781 | 737,781 | 677,317 | 410,536 | 60,464 | 3655,895 | ||
| 268,636 | 723,364 | 678,240 | 946,876 | 45,124 | 2036,175 | ||
| 290,593 | 729,407 | 679,163 | 969,756 | 50,244 | 2524,460 | ||
| -292,448 | 682,448 | 680,087 | 387,639 | 2,361 | 5,574 | ||
| -266,781 | 621,781 | 681,010 | 414,229 | -59,229 | 3508,074 | ||
| 268,636 | 723,364 | 681,933 | 950,569 | 41,431 | 1716,528 | ||
| 290,593 | 614,407 | 682,857 | 973,450 | -68,450 | 4685,403 | ||
| -292,448 | 753,448 | 683,780 | 391,332 | 69,668 | 4853,630 | ||
| -266,781 | 720,781 | 684,703 | 417,922 | 36,078 | 1301,622 | ||
| 268,636 | 651,364 | 685,627 | 954,263 | -34,263 | 1173,953 | ||
| 290,593 | 636,407 | 686,550 | 977,143 | -50,143 | 2514,320 |
Шаг 4. Определим компоненту 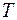 данной модели. Для этого проведем аналитическое выравнивание ряда (
данной модели. Для этого проведем аналитическое выравнивание ряда ( ) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
) с помощью линейного тренда. Результаты аналитического выравнивания следующие:
 .
.
Подставляя в это уравнение значения  , найдем уровни
, найдем уровни 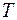 для каждого момента времени (гр. 5 табл. 4.7).
для каждого момента времени (гр. 5 табл. 4.7).
Шаг 5. Найдем значения уровней ряда, полученные по аддитивной модели. Для этого прибавим к уровням 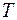 значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 4.7).
значения сезонной компоненты для соответствующих кварталов (гр. 6 табл. 4.7).
На одном графике отложим фактические значения уровней временного ряда и теоретические, полученные по аддитивной модели.

Рис. 4.6.
Для оценки качества построенной модели применим сумму квадратов полученных абсолютных ошибок.
 .
.
Следовательно, можно сказать, что аддитивная модель объясняет 97% общей вариации уровней временного ряда количества правонарушений по кварталам за 4 года.
Шаг 6. Прогнозирование по аддитивной модели. Предположим, что по нашему примеру необходимо дать прогноз об общем объеме правонарушений на I и II кварталы 2003 года. Прогнозное значение  уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
уровня временного ряда в аддитивной модели есть сумма трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
 .
.
Получим
 ;
;
 .
.
Значения сезонных компонент за соответствующие кварталы равны: 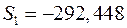 и
и  . Таким образом,
. Таким образом,
 ;
;
 .
.
Т.е. в первые два квартала 2003 г. следовало ожидать порядка 395 и 422 правонарушений соответственно.
Построение мультипликативной модели рассмотрим на данных предыдущего примера.
Шаг 1. Методика, применяемая на этом шаге, полностью совпадает с методикой построения аддитивной модели.
№ квартала,

| Количество правонарушений,

| Итого за четыре квартала | Скользящая средняя за четыре квартала | Центрированная скользящая средняя | Оценка сезонной компоненты |
| – | – | – | – | ||
| 657,5 | – | – | |||
| 655,25 | 1,3262 | ||||
| 665,5 | 1,5252 | ||||
| 708,75 | 693,75 | 0,5146 | |||
| 709,375 | 0,6640 | ||||
| 718,25 | 714,125 | 1,3891 | |||
| 689,25 | 703,75 | 1,4494 | |||
| 689,25 | 689,25 | 0,5658 | |||
| 660,5 | 674,875 | 0,5260 | |||
| 678,25 | 669,375 | 1,4820 | |||
| 690,625 | 1,3104 | ||||
| 0,6643 | |||||
| 690,5 | 687,75 | 0,6601 | |||
| – | – | – | – | ||
| – | – | – | – |
Шаг 2. Найдем оценки сезонной компоненты как частное от деления фактических уровней ряда на центрированные скользящие средние (гр. 6 табл. 4.8). Эти оценки используются для расчета сезонной компоненты 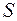 (табл. 4.9). Для этого найдем средние за каждый квартал оценки сезонной компоненты
(табл. 4.9). Для этого найдем средние за каждый квартал оценки сезонной компоненты  . Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
. Так же как и в аддитивной модели считается, что сезонные воздействия за период взаимопогашаются. В мультипликативной модели это выражается в том, что сумма значений сезонной компоненты по всем кварталам должна быть равна числу периодов в цикле. В нашем случае число периодов одного цикла равно 4.
| Показатели | Год | № квартала, 
| |||
| I | II | III | IV | ||
| – | – | 1,3262 | 1,5252 | ||
| 0,5146 | 0,6640 | 1,3891 | 1,4494 | ||
| 0,5658 | 0,5260 | 1,4820 | 1,3104 | ||
| 0,6643 | 0,6601 | – | – | ||
Всего за  -й квартал -й квартал
| 1,7447 | 1,8501 | 4,1973 | 4,2850 | |
Средняя оценка сезонной компоненты для  -го квартала, -го квартала, 
| 0,5816 | 0,6167 | 1,3991 | 1,4283 | |
Скорректированная сезонная компонента, 
| 0,5779 | 0,6128 | 1,3901 | 1,4192 |
Имеем
 .
.
Определяем корректирующий коэффициент:
 .
.
Скорректированные значения сезонной компоненты  получаются при умножении ее средней оценки
получаются при умножении ее средней оценки  на корректирующий коэффициент
на корректирующий коэффициент  .
.
Проверяем условие равенство 4 суммы значений сезонной компоненты:
 .
.
Шаг 3. Разделим каждый уровень исходного ряда на соответствующие значения сезонной компоненты. В результате получим величины  (гр. 4 табл. 4.10), которые содержат только тенденцию и случайную компоненту.
(гр. 4 табл. 4.10), которые содержат только тенденцию и случайную компоненту.

| 
| 
| 
| 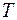
| 
| 
|
| 0,5779 | 648,9012 | 654,9173 | 378,4767 | 0,9908 | ||
| 0,6128 | 605,4178 | 658,1982 | 403,3439 | 0,9198 | ||
| 1,3901 | 625,1349 | 661,4791 | 919,5221 | 0,9451 | ||
| 1,4192 | 715,1917 | 664,7600 | 943,4274 | 1,0759 | ||
| 0,5779 | 617,7539 | 668,0409 | 386,0608 | 0,9247 | ||
| 0,6128 | 768,6031 | 671,3218 | 411,3860 | 1,1449 | ||
| 1,3901 | 713,6177 | 674,6027 | 937,7652 | 1,0578 | ||
| 1,4192 | 718,7148 | 677,8836 | 962,0524 | 1,0602 | ||
| 0,5779 | 674,8572 | 681,1645 | 393,6450 | 0,9907 | ||
| 0,6128 | 579,3081 | 684,4454 | 419,4281 | 0,8464 | ||
| 1,3901 | 713,6177 | 687,7263 | 956,0083 | 1,0377 | ||
| 1,4192 | 637,6832 | 691,0072 | 980,6774 | 0,9228 | ||
| 0,5779 | 797,7159 | 694,2881 | 401,2291 | 1,1490 | ||
| 0,6128 | 740,8616 | 697,5690 | 427,4703 | 1,0621 | ||
| 1,3901 | 661,8229 | 700,8499 | 974,2515 | 0,9443 | ||
| 1,4192 | 653,1849 | 704,1308 | 999,3024 | 0,9277 |
Шаг 4. Определим компоненту 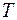 в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни
в мультипликативной модели. Для этого рассчитаем параметры линейного тренда, используя уровни  . В результате получим уравнение тренда:
. В результате получим уравнение тренда:
 .
.
Подставляя в это уравнение значения  , найдем уровни
, найдем уровни 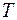 для каждого момента времени (гр. 5 табл. 4.10).
для каждого момента времени (гр. 5 табл. 4.10).
Шаг 5. Найдем уровни ряда, умножив значения 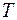 на соответствующие значения сезонной компоненты (гр. 6 табл. 4.10). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
на соответствующие значения сезонной компоненты (гр. 6 табл. 4.10). На одном графике откладываем фактические значения уровней временного ряда и теоретические, полученные по мультипликативной модели.
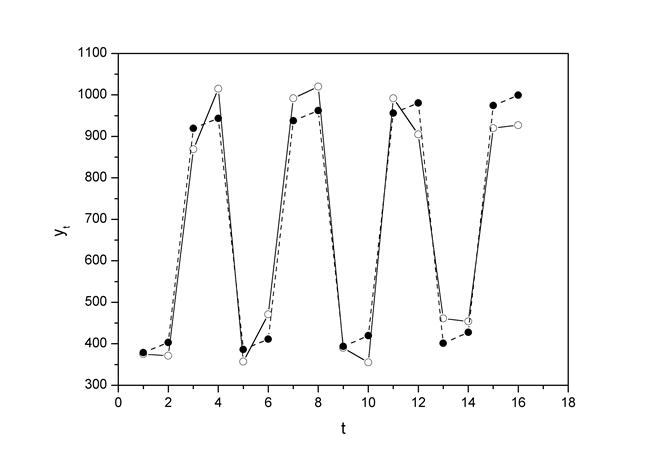
Расчет ошибки в мультипликативной модели производится по формуле:
 .
.
Для сравнения мультипликативной модели и других моделей временного ряда можно, по аналогии с аддитивной моделью, использовать сумму квадратов абсолютных ошибок  :
:
 .
.
Сравнивая показатели детерминации аддитивной и мультипликативной моделей, делаем вывод, что они примерно одинаково аппроксимируют исходные данные.
Шаг 6. Прогнозирование по мультипликативной модели. Если предположить, что по нашему примеру необходимо дать прогноз об общем объеме правонарушений на I и II кварталы 2003 года, прогнозное значение  уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
уровня временного ряда в мультипликативной модели есть произведение трендовой и сезонной компонент. Для определения трендовой компоненты воспользуемся уравнением тренда
 .
.
Получим
 ;
;
 .
.
Значения сезонных компонент за соответствующие кварталы равны:  и
и  . Таким образом
. Таким образом
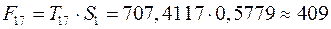 ;
;
 .
.
Т.е. в первые два квартала 2003 г. следовало ожидать порядка 409 и 436 правонарушений соответственно.
Таким образом, аддитивная и мультипликативная модели дают примерно одинаковый результат по прогнозу.
Автокорреляция в остатках может быть вызвана несколькими причинами, имеющими различную природу.
1. Она может быть связана с исходными данными и вызвана наличием ошибок измерения в значениях результативного признака.
2. В ряде случаев автокорреляция может быть следствием неправильной спецификации модели. Модель может не включать фактор, который оказывает существенное воздействие на результат и влияние которого отражается в остатках, вследствие чего последние могут оказаться автокоррелированными. Очень часто этим фактором является фактор времени  .
.
От истинной автокорреляции остатков следует отличать ситуации, когда причина автокорреляции заключается в неправильной спецификации функциональной формы модели. В этом случае следует изменить форму модели, а не использовать специальные методы расчета параметров уравнения регрессии при наличии автокорреляции в остатках.
Один из более распространенных методов определения автокорреляции в остатках – это расчет критерия Дарбина-Уотсона:
 . (4.5)
. (4.5)
Т.е. величина 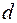 есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
есть отношение суммы квадратов разностей последовательных значений остатков к остаточной сумме квадратов по модели регрессии.
Можно показать, что при больших значениях  существует следующее соотношение между критерием Дарбина-Уотсона
существует следующее соотношение между критерием Дарбина-Уотсона 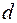 и коэффициентом автокорреляции остатков первого порядка
и коэффициентом автокорреляции остатков первого порядка  :
:
 . (4.6)
. (4.6)
Таким образом, если в остатках существует полная положительная автокорреляция и  , то
, то  . Если в остатках полная отрицательная автокорреляция, то
. Если в остатках полная отрицательная автокорреляция, то 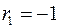 и, следовательно,
и, следовательно,  . Если автокорреляция остатков отсутствует, то
. Если автокорреляция остатков отсутствует, то  и
и  . Т.е.
. Т.е.  .
.
Алгоритм выявления автокорреляции остатков на основе критерия Дарбина-Уотсона следующий. Выдвигается гипотеза  об отсутствии автокорреляции остатков. Альтернативные гипотезы
об отсутствии автокорреляции остатков. Альтернативные гипотезы  и
и  состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение E) определяются критические значения критерия Дарбина-Уотсона
состоят, соответственно, в наличии положительной или отрицательной автокорреляции в остатках. Далее по специальным таблицам (см. приложение E) определяются критические значения критерия Дарбина-Уотсона 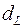 и
и  для заданного числа наблюдений
для заданного числа наблюдений  , числа независимых переменных модели
, числа независимых переменных модели  и уровня значимости
и уровня значимости  . По этим значениям числовой промежуток
. По этим значениям числовой промежуток  разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью
разбивают на пять отрезков. Принятие или отклонение каждой из гипотез с вероятностью  осуществляется следующим образом:
осуществляется следующим образом:
 – есть положительная автокорреляция остатков,
– есть положительная автокорреляция остатков,  отклоняется, с вероятностью
отклоняется, с вероятностью 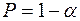 принимается
принимается  ;
;
 – зона неопределенности;
– зона неопределенности;
 – нет оснований отклонять
– нет оснований отклонять  , т.е. автокорреляция остатков отсутствует;
, т.е. автокорреляция остатков отсутствует;
 – зона неопределенности;
– зона неопределенности;
 – есть отрицательная автокорреляция остатков,
– есть отрицательная автокорреляция остатков,  отклоняется, с вероятностью
отклоняется, с вероятностью 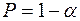 принимается
принимается  .
.
Если фактическое значение критерия Дарбина-Уотсона попадает в зону неопределенности, то на практике предполагают существование автокорреляции остатков и отклоняют гипотезу  .
.
Пример. Проверим гипотезу о наличии автокорреляции в остатках для аддитивной модели нашего временного ряда. Исходные данные и промежуточные расчеты заносим в таблицу:
Таблица 4.11

| 
| 
| 
| 
| 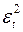
|
| -5,252 | – | – | 27,584 | ||
| -35,843 | -5,252 | 935,8093 | 1284,7 | ||
| -74,183 | -35,843 | 1469,956 | 5503,1 | ||
| 48,937 | -74,183 | 15158,53 | 2394,8 | ||
| -26,946 | 48,937 | 5758,23 | 726,09 | ||
| 60,464 | -26,946 | 7640,508 | 3655,9 | ||
| 45,124 | 60,464 | 235,3156 | 2036,2 | ||
| 50,244 | 45,124 | 26,2144 | 2524,5 | ||
| 2,361 | 50,244 | 2292,782 | 5,574 | ||
| -59,229 | 2,361 | 3793,328 | 3508,1 | ||
| 41,431 | -59,229 | 10132,44 | 1716,5 | ||
| -68,450 | 41,431 | 12073,83 | 4685,4 | ||
| 69,668 | -68,45 | 19076,58 | 4853,6 | ||
| 36,078 | 69,668 | 1128,288 | 1301,6 | ||
| -34,263 | 36,078 | 4947,856 | |||
| -50,143 | -34,263 | 252,1744 | 2514,3 | ||
| Сумма | -0,002 | 50,141 | 84921,85 | 37911,97 |
Фактическое значение критерия Дарбина-Уотсона для данной модели составляет:
 .
.
Сформулируем гипотезы:  – в остатках нет автокорреляции;
– в остатках нет автокорреляции;  – в остатках есть положительная автокорреляция;
– в остатках есть положительная автокорреляция;  – в остатках есть отрицательная автокорреляция. Зададим уровень значимости
– в остатках есть отрицательная автокорреляция. Зададим уровень значимости  . По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений
. По таблице значений критерия Дарбина-Уотсона определим для числа наблюдений 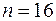 и числа независимых параметров модели
и числа независимых параметров модели  (мы рассматриваем только зависимость от времени
(мы рассматриваем только зависимость от времени  ) критические значения
) критические значения  и
и  . Фактическое значение
. Фактическое значение 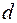 -критерия Дарбина-Уотсона попадает в интервал
-критерия Дарбина-Уотсона попадает в интервал  (1,37<2,24<2,63). Следовательно, нет основания отклонять гипотезу
(1,37<2,24<2,63). Следовательно, нет основания отклонять гипотезу  об отсутствии автокорреляции в остатках.
об отсутствии автокорреляции в остатках.
Существует несколько ограничений на применение критерия Дарбина-Уотсона.
1. Он неприменим к моделям, включающим в качестве независимых переменных лаговые значения результативного признака.
2. Методика расчета и использования критерия Дарбина-Уотсона направлена только на выявление автокорреляции остатков первого порядка.
3. Критерий Дарбина-Уотсона дает достоверные результаты только для больших выборок.
Приложение A[6]