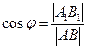Взаимное расположение точки и прямой
Если точка лежит на прямой, то ее проекции должны лежать на одноименных проекциях этой прямой:
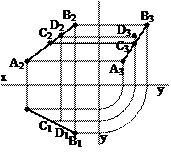
|
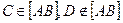
Когда прямая и точка расположены в плоскости параллельной какой-либо из плоскостей pi, то вопрос об их взаимном отношении может быть решен при построении проекций на плоскость pi.
Одним из свойств параллельного проецирования является свойство пропорциональности, т.е. если точка делит отрезок прямой в данном отношении, то проекции этой точки делят одноименные проекции прямой в том же отношении. Таким образом, чтобы на комплексном чертеже разделить отрезок в каком-то отношении, необходимо разделить в соответствующим отношении проекции этого отрезка.
 Определение длины отрезка прямой и угла ее наклона к плоскости проекции
Определение длины отрезка прямой и угла ее наклона к плоскости проекции
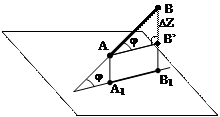
Длину отрезка прямой AB можно определить из прямоугольного треугольника AB’B, в котором:
- катет AB’=A1B1 (проекция отрезка AB на плоскость p1);
- катет BB’=DZ – разность расстояний точек A и B от плоскости p1.
 Угол j в том же треугольники определяет угол наклона отрезка прямой к плоскости p1.
Угол j в том же треугольники определяет угол наклона отрезка прямой к плоскости p1.
Аналогично для p2 и p3.
На комплексном чертеже длина отрезка A1B0 будет равна длине отрезка AB, а угол j - это угол наклона прямой к плоскости p1. Точка B0 получена путем построения отрезка B1B0, перпендикулярного A1B1 и равного DZ.

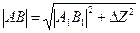 ,
,