Лекция 1. Описательная статистика.

 

Термин “статистика” имеет несколько интерпретаций:

1. Первоначально использовался для числовых данных, по которым делались выводы;

2. В дальнейшем этот термин использовался для обозначения массива числовой информации (более целесообразно для этой цели использовать термин - описательная статистика);

3. Математическая статистика - является основой методов, служащих для принятия решения в условиях неопределенности. Неопределенность, присутствующая в статистических задачах носит объективный характер и выражена в числовой форме (поэтому иногда термин “статистика” употребляется, как числовая характеристика некоторого множества данных), тогда как принятие решения зависит от исследователя;

4. Обычно при решении задач по математической статистике сначала рассматривается теория вероятности и описательная статистика и лишь после этого теория статистических выводов;

5. Выражение “статистический вывод” применяют для обозначения в математической статистике аспекта, связанного с принятием решения.

Требования к данным.

Основные требование к данным: массовость опробования, случайность опробования и предпосылка выполнения свойства эргодичности, когда каждая отдельная реализация случайной величины достаточной продолжительности, может заменить множество реализаций той же общей продолжительности и наоборот множество реализаций ограниченной продолжительности -“выборка” при обработке данных могут заменить одну реализацию достаточной продолжительности - «совокупность”. В предыдущем предложении были перечислены статистические термины (подчеркнутые), которые требуют своего определения.

Случайная величина - это такая переменная величина, которая в результате эксперимента может принять то или иное значение.

Совокупность или чаще ее называют генеральная совокупность - это все рассматриваемое нами количество наблюдений (оно может быть конечным и бесконечным).

Реализация (единичное событие, единичное наблюдение, исход опыта) - это фиксированное единичное значение случайной величине в определенной точке (пространства, времени), которую поэтому иногда называют “точечной оценкой”.

Выборка - это некоторое подмножество генеральной совокупности (конечное подмножество).

Виды данных::

Количественные данные - бывают дискретные (экзаменационная оценка) и непрерывные (вес, рост человека).

Качественные данные иногда называют категоризированные, они получаются путем сортировки данных на группы по категориям (обычно - это символьные /различный геологический возраст/ или числовые характеристики /первый, второй и т.д. горизонты, зональные изменения параметров/).

Первый этап обработки данных включает: составление массива данных, группировка на классы, ранжирование данных (перестановка в порядке убывания или возрастания). Основным понятием при статистическом моделировании является понятие о вероятности случайного события.

Вероятность есть число, которое связывается с событием в соответствии с некоторыми правилами.

Классическое определение вероятности: Вероятность события есть отношение числа возможных исходов, благоприятствующих событию к общему числу возможных исходов, при условии, что события взаимно исключают друг друга, и что они являются равновозможными. Последнее условие накладывает довольно жесткие ограничения на наблюдаемые данные, что и определяет недостаток классического определения. Более удовлетворительную формулировку определения вероятности при работе с реальными массивами данных можно дать через предельную относительную частоту (относительная частота - это абсолютное значение частоты события деленное на общее число наблюдений /всех событий/ в выборке): Пусть A событие и N(A) есть число случаев, в которых произошло событие Aв серии изN испытаний. Тогда N(A) деленное на N,есть относительная частота - при больших сериях испытаний (измерений) стремится к некоторому пределу называемому вероятностью события A и обозначается P(A).

Соотношение, устанавливающее связь между возможными значениями случайной величины и соответствующими вероятностями, называется законом или функцией распределения.

Функция распределения случайной величины(A) как непрерывной, так и дискретной есть вероятность события, заключающего в том, что в результате единичного эксперимента a из A(a €{ A}) /читается, апринадлежит множествуА/, примет значение меньшее или равное x, причем функция определена для всехX из области значений случайной величиныА.

Таким образом, функция распределения F(x) - выражает вероятность того, что выборочное значение случайной величины (a),окажется меньше некоторого заданного числа x € Aт.е. P(a < x) =F(x)(1.1).

Так как P - вероятность, изменяется от 0 - абсолютно невозможное событие, до 1 - вероятность достоверного события, то и функция распределения изменяется в этих же пределах 0 < F(x) < 1.

Функция плотности распределения случайной величины характеризует вероятность попадания выборочного значения,ав некоторый заданный интервал:

x<a<x+Dx, для непрерывной величины P(x<a<x+dx) = f(x)dx(1.2).

Иногда приведенные в двух видах законы распределения случайной величины называют соответственно интегральной и дифференциальной функцией распределения, которые связаны между собой соотношением:

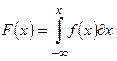, причем при x® +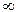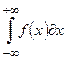=1.

Наиболее существенные особенности распределения случайной величины могут быть выражены с помощью числовых характеристик распределения. Различают точечные и интервальные значения параметров функции распределения случайной величины.

Рассмотрим наиболее распространенное распределение - нормальное:

Интегральная форма этого распределения:

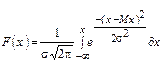(1.3) - (функция нормального распределения)

где Mx и s - параметры

Мх -математическое ожидание; s²- дисперсия.

Функция плотности распределения соответственно равна:

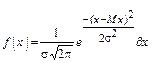(1.4) - ( функция распределения Гаусса).

Если Mx=0, а s=1, то функция распределения будет равна:

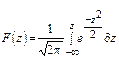(1.5) – (распределения стандартизованной нормальной величиныz=ïx-Mxï/s

Интеграл вероятности /или функция распределения/ Лапласа связан с распределением нормальной величины следующим соотношением: Обозначим черезt = x-Mx /sзначенияz>0, тогда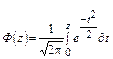(1.6) – (функция распределения Лапласа)

где t значения на числовой оси от 0 до + ,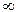

Связь с распределением стандартизованной величины будет: Ф(z)=F(z) - 1/2.(1.7)

Функция ошибок 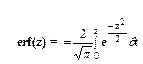(1.8)

связана со стандартизованной величинойF(z) = 1/2 (1 + erf (z);(1.8)

Значения функции стандартизованного распределения, функции Лапласа и функции ошибок, могут быть рассчитаны одна из другой по формулам 1.7 – 1.8, табулированы и их таблицы приведены в справочниках. Значения этих функций рассчитаны исходя из разложения в ряды: e^t = 1 + t+ t²/2! + t³/3! + ... , где - 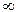<t<+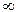

_e (^-t²_/^/₂) = 1 - t²/2 + t⁴/2² x 2! - t⁶/2³ x 3! +... (1.9)

Особенности распределения случайной величины выражаются с помощью числовых характеристик. Различают точечные и интервальные характеристики. Рассмотрим сначала точечные характеристики.

Максимум функции плотности распределения соответствует в точкеХ=Мх = 1/sÖ2p - математическое оожидания;точки перегиба графика плотности распределения соответствуют х₁=Мх -s; х₂= Мх+s,где s² - дисперсия.Графики функции нормального распределения (интегральной и дифференциальной) рассматриваются на основе анализа формул (1.3-1.5).При измененииМх график жестко смещается вдоль оси Х. При изменении s график вытягивается (s=1/2) или выполаживается (если, например, увеличить s в 2 раза).

Помимо математического ожидания и дисперсии существуют другие точечные характеристики или параметры расположения и рассеяния функции распределения. К первым относятся модаимедиана. Медиана это такая оценка функции распределения (т.е. значение случайной величины Х) при которой F(x)=1/2.В выборках это середина ранжированного ряда. Мода - наиболее распространенное значение случайной величины; распределения бывают одно, двух, полимодальные.

Для оценки точечных параметров распределения вводятся понятия начального и центрального момента: начальный момент - m^r = Mx^r ; центральный момент - m_r = M(x-Mx)^r , где под моментом понимается сумма отклонений единичных значений случайной величины от любого заданного числа – а. Из определения видно, что характеристикой математического ожидания является начальный момент первого порядка:m¹=Mx¹; а дисперсии - центральный момент второго порядка:m₂=M(x-Mx)² = s².При m₃ = å(x_i - Мx)³ -характеристикаасимметрии. Коэффициент асимметрии определяется как: Cs= m₃ /m₂ ^3/2 = m₃/s³. При нормальном распределении коэффициент асимметрии равен нулю, при Cs>0право асимметричный график гауссовой кривой (длинный правый хвост) - положительная асимметрия, соответственно при Cs<0лево асимметричный график гауссовой кривой (длинный левый хвост ) - отрицательная асимметрия.

m₄ = å(x_i - Мх)⁴ - эксцесс -характеристика крутизны графика плотности нормального распределения. Коэффициент эксцесса: Ae= E -3 =0 (где E = m₄/m₂ ² = m₄/s⁴).

Основные параметры нормального распределения (математическое ожидание и дисперсия) используются при определении интервальных оценок распределения, при этом решаются задачи двух типов:

Задача 1. Найти вероятность того, что нормально распределенная случайная величина Х с параметрами N(Mx, s)отличается от своего математического ожидания по абсолютной величине не более чем на ± e: R(úх-Mх÷£e)=2F(e/s)-1.

Еслиe=s то R=0.68268; еслиe=2s то R=0.95450; еслиe=3s то R=0.9973. Таким образом случайная величина с нормальным распределением практически не принимает значения, которые отличались бы от математического ожидания (среднего значения при n®¥) больше чем на 3s (правило 3s - по закону больших чисел Чебышева).

С другой стороны если Р =2F(e/s)-1= 0.95(вероятность 95% или 5% ошибки),тоФ=0.975,что соответствует для нормированной функцииЛапласаZ(0,1)значению1.96.

Таким образом, для 95% вероятности математическое ожидание для нормально распределенной случайной величины не будет превышатьМх±1.96s - доверительный интервал или интервальная характеристика распределения.

Задача 2. Найти вероятность того, что нормально распределенная случайная величина Х с параметрами N(Mx, s) принимает значения в пределах заданного интервала интервале [a,b]:

P(a<x<b) =Ф(b-Mx/s) - Ф(a-Mx/s);

В данном случае решается обратная задача вероятности попадания случайной величины в заранее заданный интервал (границы) изменения.