Аналитическое представление кривых и поверхностей
Пусть на плоскости задана декартова система координат.
Кривая на плоскости - это геометрическое место точек 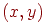 , удовлетворяющих уравнению
, удовлетворяющих уравнению

| (3.10) |
где  - функция двух переменных. Ясно, что далеко не каждая функция будет задавать линию. Так, например, уравнению
- функция двух переменных. Ясно, что далеко не каждая функция будет задавать линию. Так, например, уравнению

не удовлетворяет ни одна точка плоскости, а уравнению

удовлетворяет только одна точка  .
.
Для аналитического представления кривой во многих случаях удобнее задавать кривую параметрическими уравнениями, используя вспомогательную переменную (параметр)  :
:

| (3.11) |
где  и
и  - непрерывные функции на заданном интервале изменения параметра. Если функция
- непрерывные функции на заданном интервале изменения параметра. Если функция  такова, что можно выразить
такова, что можно выразить  через
через  , то от параметрического представления кривой легко перейти к уравнению (3.10):
, то от параметрического представления кривой легко перейти к уравнению (3.10):

Систему уравнений (3.11) можно записать в векторном виде:

Отрезок прямой представляет собой частный случай кривой, причем параметрическое представление его может иметь вид

или

Окружность радиуса  с центром в точке
с центром в точке  может быть представлена параметрическими уравнениями
может быть представлена параметрическими уравнениями

Перейдем к трехмерному пространству с заданной декартовой системой координат.
Поверхность в пространстве - это геометрическое место точек  , удовлетворяющих уравнению вида
, удовлетворяющих уравнению вида

| (3.12) |
Так же как и в случае кривой на плоскости, не всякая функция  описывает какую-либо поверхность. Например, уравнению
описывает какую-либо поверхность. Например, уравнению

не удовлетворяет ни одна точка пространства. Поверхность также может быть задана в параметрическом виде, но в отличие от кривой для этого требуются две вспомогательные переменные (параметры):

| (3.13) |
Например, сфера радиуса  с центром в точке
с центром в точке  может быть задана уравнением
может быть задана уравнением

либо же параметрическими уравнениями

Кривую в пространстве можно описать как пересечение двух поверхностей, т.е. с помощью системы уравнений

| (3.14) |
или параметрическими уравнениями вида

| (3.15) |