Средней точки
Алгоритм построения окружности методом
Рассмотрим уравнение окружности радиуса 
с центром в начале координат
(4.6)
Введем в рассмотрение функцию окружности
(4.7)
Любая точка 
,которая лежит на окружности удовлетворяет уравнению
Если точка находится внутри круга, то функция окружности будет иметь отрицательное значение. Если точка лежит за пределами круга, значение функции окружности будет положительным. Подытоживая, можно сказать, что относительное положение любой точки с координатами )определяется проверкой знака функции окружности:
(4.8)
Проверка выполняется на каждом этапе выборки для средних положений между пикселями вблизи заданной окружности. Таким образом, функция окружности – это параметр принятия решения в алгоритме средней точки, и для этой функции можно установить операции приращения, как это было сделано для алгоритма построения прямой линии.
На рис. 4.1 показана средняя точка между двумя возможными пикселями в точке выборки. Предположим, что мы только что поставили точку в пикселе с координатами 
Теперь нужно определить, какой из двух пикселей ближе к заданной окружности — пиксель с координатами 
или пиксель с координатами 
Параметром принятия решения будет функция окружности (4.7), которая рассчитывается для средней точки между этими двумя пикселями:
Рис.4.2
В случае, когда 
, полагаем 
(если средняя точка внутри окружности, то она (окружность) ближе к верхнему пикселу). Тогда
где
При этом
Тогда
, 
, 
,
для
В случае, когда 
, делаем шаг вниз(если средняя точка вне окружности, то она(окружность) ближе к нижнему пикселу), полагая 
. Тогда
,
где
Для рассматриваемого случая, когда , 
получаем
При этом
Тогда
Таким образом
, 
,
для
Рассмотрим алгоритмы вычисления 
и 
для случая, когда , 
.
В этом случае
И выражение для 
принимает вид
Таким образом, если , то
,
если , то
Для удобства заменим в выражениях для 
и 
на 
, тогда
для
При получаем
Начальные значения параметров 
и 
определим из условия 
и 
Тогда
Поскольку радиус и приращение, 
целые числа, то значение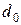 
можно округлить и принять
Подводя итог изложенному, запишем в собранном виде алгоритм построения окружности методом средней точки.
Установить начальные значение для 
Поставить начальные точки
Выполнять в цикле пока 
если , то
если , то
Поставить точки, соответствующие текущему шагу (рис. 4.3)
Рис. 4.3
Приводимая ниже функция расставляет точки окружности, соответствующие текущему шагу.
void CirclePoints(CDC& dc,int x,int y,CPoint &P,COLORREF color)
{
dc.SetPixel(x+P.x,y+P.y,color); //1
dc.SetPixel(y+P.x,x+P.y,color); //2
dc.SetPixel(y+P.x,-x+P.y,color); //3
dc.SetPixel(x+P.x,-y+P.y,color); //4
dc.SetPixel(-x+P.x,-y+P.y,color); //5
dc.SetPixel(-y+P.x,-x+P.y,color); //6
dc.SetPixel(-y+P.x,x+P.y,color); //7
dc.SetPixel(-x+P.x,y+P.y,color); //8
}
Приводимая ниже функция реализует алгоритм построения окружности методом средней точки.
void MyCircle(CDC& dc,CPoint &P,int r,COLORREF color)
{
int x=0;
int y=r;
int d=1-r;
int p=3;
int q=-2*r+5;
CirclePoints(dc,x,y,P,color);
while(y>x)
{
if(d<0)
{
d+=p;
p+=2;
q+=2;
x++;
}
else
{
d+=q;
p+=2;
q+=4;
x++;
y--;
}
CirclePoints(dc,x,y,P,color);
}
}