Построение аксонометрических проекций геометрических фигур. Прямоугольная изометрия. Построение аксонометрического куба.
Прямоугольная аксонометрическая проекция окружности, лежащей в плоскости проекций (вывод).
Прямоугольной аксонометрической проекцией окружности, лежащей в некоторой плоскости общего положения, составляющей 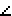
 , не равный 0 и 90
, не равный 0 и 90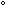 , с картинной плоскостью Q, будет эллипс.
, с картинной плоскостью Q, будет эллипс.
Большая ось этого эллипса есть проекция того диаметра окружности, который параллелен прямой пересечения плоскости P, в которой лежит окружность, и плоскости Q. Малая ось эллипса расположена перпендикулярно [MN].
[MN]=Q P; Б.О.Э.
P; Б.О.Э.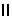 [MN]; М.О.Э.
[MN]; М.О.Э.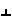 [MN].
[MN].
В практике построения аксонометрических проекций деталей машин особенно часто встречаются проекции окружности, лежащей в плоскостях проекций H, V, W или им параллельных.
Аксонометрической проекцией окружности является эллипс. Для его построения необходимо найти оси, т.е. найти их размер и направление.
 Рис.7
Рис.7
| [AB]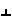 [CD]; S [CD]; S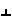 Q; [A0B0] Q; [A0B0]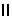 h; [C0D0] h; [C0D0]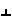 h; [A0B0]=d; [C0D0]=dcos h; [A0B0]=d; [C0D0]=dcos
|
Задача свелась к определению cos через соответствующий коэффициент искажения.
через соответствующий коэффициент искажения.
Рассмотрим эту же картинку, заданную двумя пересекающимися прямыми (z z0)
z0)
 Рис.8
Рис.8
| М.О.Э.=|C0D0|=CDsin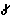 0; cos 0; cos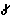 0=r 0=r 
|
Правило:
"Окружности, расположенные в плоскостях проекций или им параллельных, проецируются на картинную плоскость в виде эллипса, большая ось которого перпендикулярна к той аксонометрической оси, которая является проекцией ортогональной оси, перпендикулярной плоскости проецируемой окружности, а малая ось эллипса параллельна этой аксонометрической оси."
Для наглядности при определении направлений осей эллипсов и их размеров впишем окружности в грани куба со стороной |d|, параллельные плоскостям проекций.
 Рис.9
Рис.9
|
Т.к. плоскости проекций H, V и W в прямоугольной изометрии одинаково наклонны к картинной плоскости, коэффициенты искажения по осям одинаковы и эллипсы (аксонометрические проекции окружностей, расположенных в плоскостях проекций и им параллельным) будут конгруэнтны.
p = r = q = 0.82 (1)
Для простоты построений ГОСТ 2317-69 предлагает пользоваться приведёнными коэффициентами искажения:
p = r = q = 1 (2)
В этом случае получается не натуральная аксонометрическая проекция, а проекция, увеличенная в 1.22 раза.
В 1 случае Б.О.Э.=d; М.О.Э.=d =0.58d
=0.58d
Во 2 случае Б.О.Э.=1.22d; М.О.Э.=0.58*1.22d=0.7d
М.О.Э. по направлению совпадает со свободной аксонометрической осью, а Б.О.Э. ей перпендикулярна. Следовательно, направление осей эллипсов совпадает с направлением диагоналей граней куба.
Кроме точек на осях, отметим ещё 4 точки, принадлежащие эллипсу. Это точки, где вписанная окружность касается рёбер куба. Т.к. касание является инвариантом параллельного проецирования, эллипсы будут касаться куба в этих же точках.
Пример. Дано: Шестигранная пустотелая призма.
Нужно: Построить эту призму с разрезом в прямоугольной изометрии, применив приведённый коэффициент искажения.
Для перевода истинного размера в приведённый (увеличенный) пользуются угловым масштабом.