Определение линий пересечения поверхностей вращения с помощью секущих плоскостей.

Вспомогательные плоскости частного положения применяются в тех случаях, если соответствующие оси поверхностей либо параллельны, либо перпендикулярны к тем или иным плоскостям проекций.

Пример 1. Дано: 2 цилиндра вращения, у которых оси скрещиваются в пространстве. Ось большого цилиндра перпендикулярна к W, малого - к H.

Нужно: Построить линию пересечения.

Отметим точки, не требующие специального построения. Введём плоскости-посредники P1, P2, P3, P4 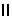V (так, чтобы оба цилиндра пересекались с ними по своим образующим).

На профильной плоскости проекций мы видим, что точки:

  • 1 - низшая точка видимой части линии пересечения
  • 2 - низшая точка невидимой части линии пересечения
  • 3, 4 - высшие точки линии пересечения
  • 5, 6 - точки, определяющие границу видимости на плоскости V.
  • Вводя плоскости-посредники S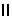H, найдём дополнительные точки сечения, например, 7 и 8.
Рис.1

 

 
 

Рис.2

Если цилиндры разных диаметров, но оси пересекаются, то получим совпадение видимой и невидимой частей линии пересечения. d < D.

Рис.3

 

Рис.4

Если d=D, то фронтальная проекция линии пересечения представляет собой две пересекающиеся прямые, которые являются фронтальными проекциями плоских кривых - эллипсов.

Рис.5

 

Рис.6

Пример 2. Дано: Прямой круговой усечённый конус, расположенный вертикально (на H) и цилиндр, расположенный горизонтально (на W). Оси цилиндра и конуса пересекаются в точке O.

Нужно: Построить их линию пересечения.

Как и в предыдущем примере, определяем сначала характерные точки линии пересечения:

  • A и B - высшая и низшая точки
  • C и D - точки, определяющие видимость линии пересечения на плоскости проекций H.
  • Если взять в качестве вспомогательных плоскостей фронтальные или профильные плоскости, то они пересекут конус по гиперболам, а не по простым линиям, как требуется для построения. Следовательно, такие плоскости неудобны. Вспомогательные горизонтальные плоскости T пересекают конус по окружностям, а цилиндр - по образующим. Та и другая линия - простые. Искомые точки (E, F, K, L) находим на пересечении образующих с окружностями.
Рис.7

 

Рис.8