Совмещение - вращение вокруг следа плоскости.
Совмещение является частным случаем вращения плоскости вокруг горизонтали или фронтали. При совмещении за ось вращения принимается не произвольная горизонталь или фронталь плоскости, а её горизонтальный или фронтальный след (нулевые горизонталь или фронталь). В этом случае в результате поворота плоскости она совпадает (совмещается) с плоскостью проекций H, если вращение осуществляется вокруг горизонтального следа плоскости, либо с V при вращении её вокруг фронтального следа.
Метод совмещения применяется тогда, когда требуется определить истинный вид геометрических фигур или построить в плоскости общего положения фигуры заданной формы и размеров.
Задача. Совместим плоскость Q общего положения, заданную следами, вращением вокруг следа QH с плоскостью H.
 Рис.4
Рис.4
|
При этом преобразовании след QH как ось вращения остаётся на месте. Поэтому для нахождения совмещённого положения плоскости достаточно найти совмещённое положение только одной принадлежащей ей точки (не лежащей на следе QH).
В качестве такой точки целесообразно (для упрощения геометрических построений) взять точку, принадлежащую фронтальному следу QV.
Точка A при вращении вокруг оси QH будет перемещаться по дуге окружности, принадлежащей плоскости S, перпендикулярной к оси вращения
(S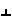 H)
H)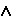 (SH
(SH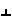 QH)
QH)
Следует отметить, что совмещённое положение точки A и следа QV-QV0 (да и любой точки, принадлежащей плоскости Q) можно построить, не пользуясь центром и радиусом вращения. Для этого достаточно из точки Qx описать дугу радиусом, равным расстоянию |QxA2| до её пересечения с прямой (горизонтальным следом SH плоскости S, в которой будет перемещаться точка A), проведённой через A1 перпендикулярно к QH. Через полученную точку пройдёт фронтальный след плоскости QV0 при совмещении его с плоскостью H.
Это следует из того, что любая геометрическая фигура, лежащая в плоскости Q, при её совмещении с плоскостью H проецируется в конгруэнтную фигуру.
(Ф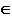 Q)
Q)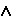 (Ф
(Ф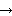 Ф0)
Ф0) 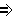 Ф
Ф Ф0; [A2Qx]
Ф0; [A2Qx] [A0Qx]
[A0Qx]
 Рис.5
Рис.5
|
Пример: Дана плоскость Q общего положения и фронтальная проекция  ABC, лежащего в этой плоскости. Вращением вокруг горизонтального следа QH определить истинную величину
ABC, лежащего в этой плоскости. Вращением вокруг горизонтального следа QH определить истинную величину  ABC.
ABC.
 Рис.6
Рис.6
|
| V ОБРАЗОВАНИЕ И ИЗОБРАЖЕНИЕ ПОВЕРХНОСТЕЙ 1. Классификация поверхностей. Задание поверхности на комплексном чертеже. 2. Линейчатые поверхности: 2.1 Циллиндрическая поверхность. 2.2 Коническая поверхность. 2.3 Цилиндроид, коноид, косая плоскость. 3. Поверхности вращения: 3.1 Однополостный гиперболоид. 3.2 Двухполостный гиперболоид. 3.3 Тор. 4. Винтовые поверхности. | Лекции: 1 2 3 4 5 6 7 8 9 10 11 12 13 |