Лекция 2 Теорема Остроградского-Гаусса
§ 2 – 1 Теорема Остроградского-Гаусса.

| Полный поток вектора напряженности электрического поля через любую замкнутую поверхность с точностью до коэффици-ента 1/e0 равен алгебраической сумме зарядов, находящихся вну-три этой поверхности. Доказательство этого утверждения проводится в три этапа. Сначала теорема доказывается для точечного заряда и выпуклой поверхнос-ти.Затем рассматривается поверхность любой формы, наконец , до-казательство формулируется для системы зарядов. |
1. Рассмотрим точечный заряд Q. Опишем вокруг его воображаемую сферу и вычислим полный поток через эту поверхность. Для вычисления используем определение телесного угла dW (см. рис.4):
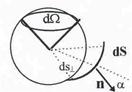 Рис.4.Телесный угол.
Рис.4.Телесный угол.
|   ;
Ф = ;
Ф =  = 4p E R2,
т.к. в подинтегральном выражении величины E и R, а полный телесный угол равен 4p. Подставляя вместо Е определение напря-женности поля для точечного заряда Q, находим, что = 4p E R2,
т.к. в подинтегральном выражении величины E и R, а полный телесный угол равен 4p. Подставляя вместо Е определение напря-женности поля для точечного заряда Q, находим, что
|
Ф =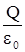 .
.
 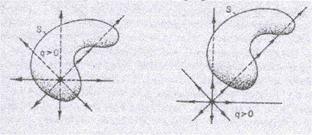 Рис.5. Различные формы прверхностей
Рис.5. Различные формы прверхностей
| Видно, что результат не зависит от радиуса сферы. Если поверхность несферическая, но выпуклая, то, как известно из стериометрии, dScosa = dS = dSn (см.рис.4), и вновь ре-зультат оказывается прежним. 2. Если поверхность интегрирования имеет произвольную форму, то для заряда внутри поверхности линии напряженности пересе- |
кают ее нечетное количество раз (один или три) (см. рис.5), причем косинус угла между вектором напряженности и внешней нормалью к поверхности будет два раза положитель-ным и один раз отрицательным ( угол a - тупой), так что два слагаемых общего потока компенсируют друг друга.
Если же заряд находится вне поверхности, то поток пересекает ее четное количество раз (два, четыре и т.д) так, что положительные и отрицательные ( для тупых углов между n и Е) слагаемые уничтожают друг друга и общий поток оказывается равным нулю.


 3. Если зарядов несколько, то в силу принципа суперпозиции Е (SЕi) = S Еi ; ФS = S Фi . Для каждого заряда в отдельности теорема доказана, значит она остается справедливой и для макроскопического (конечного) заряда, который можно представить в виде суммы точеч-ных зарядов.
3. Если зарядов несколько, то в силу принципа суперпозиции Е (SЕi) = S Еi ; ФS = S Фi . Для каждого заряда в отдельности теорема доказана, значит она остается справедливой и для макроскопического (конечного) заряда, который можно представить в виде суммы точеч-ных зарядов.
Математическая форма записи теоремы Гаусса имеет следующий вид:
Ф0 = 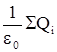 или в развернутом виде
или в развернутом виде 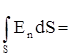
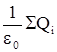 .
.
Следствие:если заряды, создающие поле, находятся вне воображаемой замкнутой поверх-ности, то поток напряженности через эту поверхность равен нулю.
Теорема Гаусса имеет достаточно важное значение, т.к. является одним из уравнений Максвелла, которые лежат в основе теории электромагнетизма. Кроме того, эта теорема может быть использована для вычисления напряженности. Для этого необходимо, чтобы величину Е можно было вынести из-под интеграла. Это можно сделать, если Е =const на всей поверхности интегрирования. Нетрудно догадаться, что воображаемая замкнутая поверхность должна иметь симметрию, подобную симметрии расположения зарядов. При этом удобно ее выбрать так, чтобы косинус угла между вектором Е и нормалью к поверхно-сти принимал значения либо 1 дибо 0. Таким условиям удовлетворяют три класса симмет-рии: сферическая, цилиндрическая и зеркальная, однако в двух последних случаях необхо-димо пренебрегать краевыми эффектами, т.к. на на краях нарушается распределение силовых линий. Ясно, что для выбора конфигурации поверхности необходимо знать, как направлен вектор Е. Здесь важно учитывать, что для статических зарядов напряженность поля вблизи зарядов должна быть перпендикулярной поверхности области распределения зарядов. В противном случае всегда будет составляющая поля, направленная вдоль поверх-ности распределения, что может вызвать электрический ток, и статическое распределение будет нарушено. Для иллюстрации полезно рассмотреть два примера.
Поле от бесконечной плоскости.
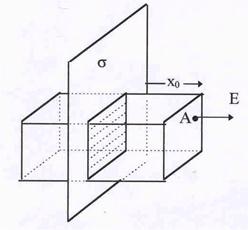 Рис.6. Поле от плоскости.
Рис.6. Поле от плоскости.
| Пусть имеется плоскость, равномерно заряженная с поверхностною плотностью s.Требуется найти напря-женность электрического поля в точке, отстоящей от плоскости на расстояние х0. Для решения задачи про-ведем замкнутую поверхность через заданную точку А (см. рис.6).Поверхность имеет форму прямоуголь-ного параллелепипеда, боковые грани которого пер-пендикулярны заряженной плоскости. Выбор такой формы поверхности связан с тем, что вектор напря-женности электрического поля Е вблизи плоскости должен быть нормален к ней. Кроме того, наша вооб-ражаемая поверхность должна быть симметричной относительно заряженной плоскости. Полный поток через поверхность параллелпипеда складывается из |
потоков через его боковую поверхность и потоков через его верхнее и нижнее основания, параллельные заряженной плоскости. Но поток через боковые поверхности равен нулю, т.к. нормали ко всем четырем боковым граням перпендикулярны вектору Е и для них cosa = =cos(n ^E) = 0. В силу симметрии потоки через верхнее и нижнее основания одинаковы так, что полный поток Ф0 = 2ЕАS. В то же время заряд, находящийся внутри нашей воображаемой поверхности равен заряду на заштрихованном (см.рис.6) участке, т.е. Q = s S. Тогда из теоремы Гаусса следует, что 2ЕАS =(1/e0) s S, откуда
ЕА =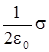 .
.
Поле от заряженной сферы.
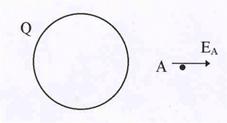 Рис.7. Поле от сферы.
Рис.7. Поле от сферы.
| В качестве второго примера рассмотрим поле от заря-женной сферы, полный заряд которой равен Q. Если точ-ка А (см. рис7) , где требуется определить напряженность, находится вне заряженной сферы, то очевидно в качестве воображаемой поверхности выбрать сферу, концентри-ческую нашей заряженной сфере. В этом случае ЕА па-раллельно n, и Ф0 = ЕАS.Т.к.площадь сферы равна 4pR2, то из теоремы Гаусса нетрудно найти: |
