Основные понятия
Системы линейных уравнений
Система m линейных уравнений с n неизвестными в общем случае имеет вид:
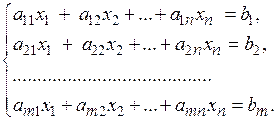(5.1)
Здесь 
– неизвестные, подлежащие определению;
– коэффициенты при неизвестных, при этом первый индекс 
указывает номер уравнения, а второй 
– номер неизвестного, при котором стоит этот коэффициент; 
– свободные члены (
; 
).
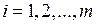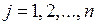Система (6.1) называется однородной, если все ее свободные члены 
равны нулю. Если хотя бы один из свободных членов отличен от нуля, то система (5.1) называется неоднородной.
Решением системы (5.1) называется такая упорядоченная совокупность чисел (
), при подстановке которой в каждое из уравнений (5.1) все уравнения системы обращаются в тождества. Решить систему (5.1) значит найти все ее решения или показать, что система решений не имеет.
Система называется совместной, если она имеет хотя бы одно решение, и несовместной, если решений системы не существует. Совместная система называется определенной, если она имеет единственное решение, и неопределенной, если решений несколько.
Примеры.
1. 
Эта система однородная, так как правые части равны нулю. Система имеет единственное решение (0,0), значит, она совместная и определенная.
Всякая однородная система линейных уравнений совместна, так как всегда имеет нулевое решение (0,0,…,0).
2. 
Эта система не имеет решений, значит, она несовместна.
Две системы с одним и тем же набором неизвестных называются равносильными в следующих случаях:
а) если каждое решение первой системы является решением второй, и каждое решение второй системы является решением первой;
б) если обе системы несовместны.
Равносильные системы уравнений должны иметь одинаковые наборы неизвестных, но число уравнений в них может и не совпадать.
Пример. Решить системы линейных уравнений:
1) 
2) 
Первая система имеет единственное решение (1;0), значит она совместная, определенная. Вторая система также совместная и определенная, так как имеет единственное решение (1;0). Эти системы равносильны, поскольку множества их решений совпадают.
Используя введенные в п.1 операции над векторами,
можно записать систему (5.1) в векторной форме. Составим матрицу
А=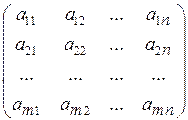
, (5.2)
элементами которой являются коэффициенты при неизвестных в системе (5.1). Вектор-столбцы
, 
, …, 
этой матрицы есть столбцы коэффициентов при неизвестных , соответственно. Обозначим через В=
– столбец свободных членов системы (5.1). Тогда систему (5.1) можно записать в виде:
, (5.3)
или
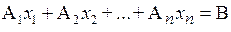. (5.4)
Уравнение (5.4) назовём векторной формой записи системы линейных уравнений (5.1). Уравнение (5.4) будем также называть системой линейных уравнений.
Совокупность чисел () является решением уравнения (5.4), если 
– верное векторное равенство. Пусть
n-мерный вектор () является решением системы уравнений (5.1), т.е. справедливы равенства
(5.5)
Так как числовые соотношения (5.5) равносильны равенству векторов 
и В, то можно утверждать, что вектор () является решением системы уравнений (5.1) тогда и только тогда, когда он является решением уравнения (5.4).
Матрица 
, или А = (А1А2… Аn),
называется основной матрицей системы линейных уравнений (5.1) (или просто матрицей системы (5.1)).
Обозначим через Х=(
) неизвестный вектор. Согласно правилу перемножения матриц произведение матриц А и Х имеет смысл, так как размер матрицы А есть 
, а размер Х – 
, и представляет собой матрицу, содержащую m строк и 1 столбец, т.е. матрицу-столбец
АХ = 
.
Система равенств (5.1) означает, что эта матрица-столбец равна матрице-столбцу В свободных членов, т.е. систему (5.1) можно записать в матричной форме: АХ = В. Вектор К = () будет решением системы (5.1) тогда и только тогда, когда АК = В – верное равенство.
Расширенной матрицей системы (5.1) называется матрица
,
или 
= (А1 А2 … Аn В), образованная из матрицы А добавлением столбца свободных членов В.
Заметим, что ранг системы векторов А1, А2, …, Аn равен рангу матрицы А системы (5.1), а ранг системы векторов А1, А2, …, Аn, В равен рангу расширенной матрицы .