Способы нахождения обратной матрицы

1. Для невырожденной матрицы А можно найти обратную, исходя из определения. Рассмотрим этот способ на примере квадратной матрицы 2-го порядка.

Пусть дана матрица А=. Определитель матрицы А, (), не равен нулю, значит, матрица А невырожденная. Найдем матрицу
А^–1=, такую, что АА^–1=Е , т.е. . Перемножая матрицы, стоящие слева, получим

По определению равных матриц имеем:

Решая эту систему уравнений, получим: .

Следовательно, матрица А^–1, обратная матрице А, имеет вид

А^–1=.

Таким образом, нахождение обратной матрицы с использованием определения сводится к решению системы n² линейных уравнений, неизвестными в которой являются n² элементов матрицы А^–1. Если эта система не имеет решений, то для матрицы А не существует обратной матрицы.

2. Нахождение обратной матрицы с помощью элементарных преобразований строк.

Составим вспомогательную матрицу С=размера , в левом блоке которой стоит квадратная матрица А порядка n, а в правом блоке – единичная матрица того же порядка. С помощью элементарных преобразований "длинных" строк матрицы С приведем ее левый блок к единичной матрице. Тогда в правом блоке преобразованной матрицы окажется матрица А^–1, обратная матрице А.

Пример. Найти матрицу, обратную матрице .

○ Составим вспомогательную матрицу и приведем ее левый блок к единичной матрице:

~ ~ .

Матрица, стоящая в левом блоке, единичная, следовательно,

А^–1=. ●

Замечание. Если в процессе нахождения обратной матрицы ступенчатый вид преобразованной матрицы А, стоящей в левом блоке, содержит нулевые строки, то ранг матрицы А будет меньше n, то есть матрица А – вырожденная и обратной матрицы не имеет.

3. Пусть дана невырожденная матрица А n-го порядка

А=,

т.е. . Рассмотрим матрицу, составленную из алгебраических дополнений элементов матрицы А:

А*=.

Матрица А* называется присоединенной, или союзной, по отношению к матрице А. Обратите внимание, что в матрице А* число расположено не в i-й строке и j-м столбце, а, наоборот, в j-й строке и i-м столбце, т.е. .

Теорема 3.8. Если А – невырожденная матрица, то матрица

В =

является обратной по отношению к матрице А.

□ Для доказательства надо проверить справедливость равенств АВ=Е и ВА=Е. Полагая АВ=С, запишем

С=АВ =×.

Согласно правилу умножения матриц, элемент матрицы С, расположенный в i-й строке и j-м столбце, равен

При это выражение равно 1, так как тогда в скобках стоит разложение определителя по элементам i-й строки; если же , то написанное выражение равно нулю, поскольку в этом случае в скобках стоит сумма произведений элементов i-й строки определителя
на алгебраические дополнения соответствующих элементов j-й строки (см. теорему 3.5). Таким образом, равно 1, если 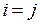, и равно нулю, если . Это означает, что С= Е. Совершенно аналогично доказывается равенство ВА = Е. ■

Из теоремы 3.8 следует, что для невырожденной матрицы обратная матрица существует.

Теорема. 3.9. Если для матрицы А существует обратная, то она единственная.

□ Предположим, что для матрицы А существуют две обратные матрицы В и В₁. По определению обратной матрицы АВ₁= Е. Умножая обе части этого равенства слева на В, получим В(АВ₁) = ВЕ. На основании свойств умножения матриц В(АВ₁) = (ВА)В₁. Но ВА = Е, значит, ЕВ₁= ВЕ, откуда следует В₁= В. ■

Замечание. Очевидно, что если матрица В является обратной для матрицы А, то А является обратной для В.

Пример. Найти матрицу, обратную матрице .