Анализ линейного режима работы ЧАПЧ
ЧАПЧ
РЕГУЛИРОВКИ В РПУ
Обратное преобразование шумов гетеродина
Преобразование в ПрЧ ГТП энергии спектра шума в полосе Dfпч благодаря действию интенсивной помехи Fп, не попадающей в полосы основного и дополнительных каналов приема.
Uшгп = (4кТy2гпRшгDfпч)0,5 - наличие помехи (5.4)
При увеличении Uп à Uшгп тоже растет, и отношение С/Ш уменьшается.
суммарный шум-
Uшг = (U2шгос +U2шгз+ U2шгг+ U2шгп) 0,5 (5.5)
ЧАПЧ; ФАПЧ; АРУ; РПП
Частотная автоподстройка частоты
пример:
fпр= 10МГц; DFпч=100кГц; fo= 400МГц;
dfc=10-5; dfг=10-3
-----
Dfосн =
Dfг =
Dfпч= (Df2осн + Df2г)0,5 =
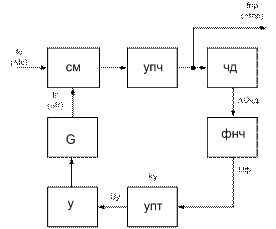
Рис.5.2 структурная схема ЧАПЧ
Любая ЧАПЧ – замкнутая система автоматического регулирования (АР) с обратной связью (ООС)
fг - fс = fпр (5.6)
+Dfг à +Dfпр (5.7)
+Dfс à -Dfпр (5.8)
Dfпр = Dfг - Dfс (5.9)
При изменении fг или fс от номинала система стремится уменьшить (нивелировать) это отклонение
+Dfг à+Dfпр à+DUуà-Dfг
+Dfс à-Dfпр à-DUуà+Dfг (5.10)
Номинальное значение промежуточной частоты определено частотой настройки ЧД
Эталон fнчд = fпч (рис. 5.3)
Система подстраивает fпр к частоте настройки ЧД fнчд
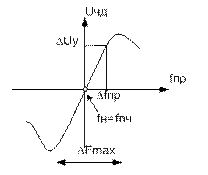

Рис.5.3 Статическая характеристика ЧД, Рис.5.4 Статическая характеристика управителя,
типовая, нелинейная нелинейная
крутизна частотной характеристики ЧД
Sчд =DU/Df на fнчд (5.11)
крутизна характеристики управителя
Sу = - Dfг/DUу на DUу =0 (5.12)
Инерционными свойствами ЧД и У можно пренебречь (tу. tчд << tф – постоянная времени ФНЧ)
Полоса пропускания фильтра мала, чтобы предотвратить демодуляцию.
Эффективность работы АПЧ характеризуется величиной остаточной ошибки на частоте Dfуcт (для статической системы)
ЕслиDfуcт =0 à система астатична.
Коэффициент автоподстройки
Кап = Dfвх/Dfуcт (5.13)
Применим операторный метод Лапласа.
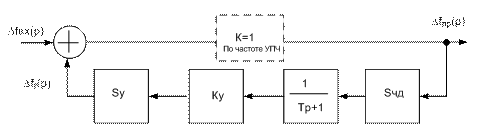
Рис.5.5 линейная модель ЧАПЧ, частный случай с ФНЧ – астатическое звено 1-го порядка
fпр= fг- fс (5.14)
Dfпр = Dfг- Dfс (5.15)
Dfвх = Dfс (Dfг) (5.16)
Операторный коэффициент передачи петли ОС (нижняя ветвь)
Kос(p)=(SчдSуKу)/(Tp+1)=Kос/(Tp+1) (5.17)
коэффициент передачи замкнутой системы с ООС
Kз(p)=K(р)/(1- Kос(p)Kр(p)) = (Tp+1)/(Tp+1- Кос) (5.18)
Tp+1- Кос- характеристическое уравнение (=0) à корни:
Po = (Кос-1)/T <0 т.к. | Кос | >1 (5.19)
-это условие устойчивости (корни в левой полуплоскости).
При Кос <0 это значит, что Sчд и Sу должны иметь разные знаки.
Тогда передаточная характеристика системы ЧАПЧ с простым RC фильтром в контуре:
Кчапч (р) =(Tp+1)/(Tp+1+ | Кос|) (5.20)
Dfпр (p) = Dfвх(p) Кчапч (р) à переходная характеристика:
Единичный скачок Dfвх; изображение по Лапласу L[Dfвх]= Dfвх/p (5.21)
Dfуcт = lim(Dfпр(t)) = lim(pDfпр(p)) =Dfвх/(1+ | Кос|)(5.22)
tà00 pà0
1-----------------------------------------1
[ т е о р е м а]
Кап = Dfвх/Dfуcт = (1+ | Кос|) не равен 0, -система статическая(5.23)

Рис.5.6 переходный процесс установления частоты
Tэ=T/ (1+ | Кос|)(5.24)
Работа ЧАПЧ при больших растройках(учет нелинейности)
Dfпр = Dfг- Dfс(5.25)
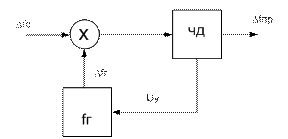
Рис.5.7 модель при нелинейном режиме
Фильтр и усилитель отнесены к ЧД
Uу = Fчд(fпр) (см. рис.5.8) (5.26)
Обратная ф-ия:
Dfпр = Qчд(Uу) (см. рис.5.9)
Dfг =Fу(Uу)(см. рис.5.10)(5.27)
где Qу–обратная функция для Fу


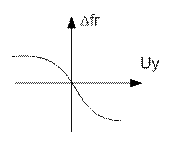
Рис.5.8 Fчд Рис.5.9 Qчд Рис.5.10 Fу
а) Dfг, Dfс, Dfпр
в уст. режиме
Dfпр = Dfг- Dfс(5.28)
Qчд (Uу) = Fу(Uу)- Dfс- нелинейное уравнение(5.29)
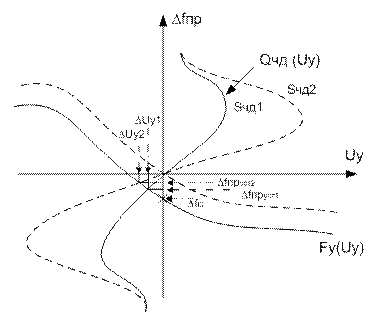
Рис.5.11 Графическое решение (5.29)
Чем выше крутизна ЧД, тем меньше Dfпруст
б) увеличиваем плавно Dfс, считая что система находится в режиме синхронизации
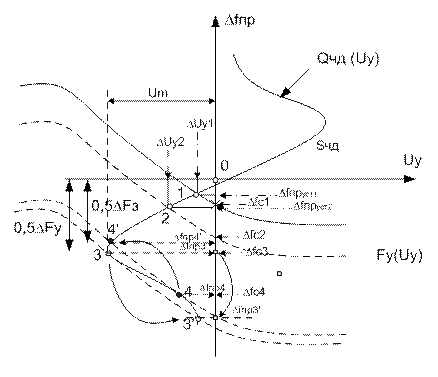
Рис.5.12 Графическое решение для DFу, D Fз
Еще два параметра DFу, D Fз, полоса удержания и полоса захвата
полоса удержания – способность сохранять режим слежения при увеличении растройки
полоса захвата – способность системы слежения входить в режим синхронизации (автоподстройки)
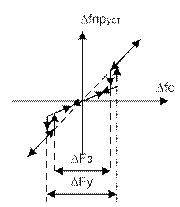
Рис.5.13 ошибка слежения от частоты растройки
DFу =2Um/Sчд +2UmSу = (2Um/Sчд) (1+ Sчд Sу)= D Fчд (1+ Sчд Sу)(5.30)
D Fз=D Fчд (приближенно)(5.31)
1) полоса удержания больше полосы захвата;
2) D Fз определяется створом частотной характеристики ЧД, полоса DFу еще и петлевым коэффициентом передачи Sчд Sу
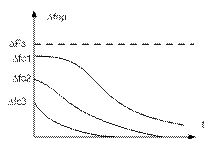
Рис.5.14 переходный процесс при захвате частоты
Пример

Рис.5.15 элементы ЧАПЧ