Шифратор

СХЕМА БЕРНУЛЛИ

Пусть A – случайное событие по от­ношению к некоторому испытанию. Будем считать, что испыта­ние имеет два исхода: наступление события A и ненаступление события A (т.е. наступление события`A). Если производится не­сколько таких испытаний, причем вероятность события A в каж­дом из них не зависит от исходов остальных, то такие испыта­ния называют независимыми (относительно события A).

Говорят, что проводимый эксперимент удовлетворяет схеме Бернулли, если:

1) эксперимент состоит из n независимых испытаний;

2) каждое испытание имеет два исхода – наступление некото­рого события A и на­ступление события`A;

3) вероятность события A в каждом испытании постоянна.

Теорема 2.10. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события A равна p, а не появления – q. Тогда вероятность P_n(k) того, что в n испы­таниях событие A появится ровно k раз, вычисляется по фор­муле Бернулли: P_n(k) = С_n^k·p^k·q^n-k.

■ Наивероятнейшее число наступления события A в n ис­пыта­ниях – число k=k₀, при котором вероятность P_n(k) явля­ется наиболь­шей.

▲Теорема 2.11. Если p¹0 и p¹1, то наивероятнейшее число k₀ можно определить из двойного неравенства: np–q £ k₀ £ np+p. Если np+p не является целым числом, то дан­ное неравенство оп­ределяет лишь одно наивероятнейшее число. Если np+p – целое число, то имеются два наивероятнейших значения: k₀¢ = np – q и k₀¢¢ = np +p.

Пример 2.18. Вероятность попадания в мишень при выстреле равна 0,8. Найти: а) вероятность того, что при семи выстрелах произойдет пять попаданий в мишень; б) наивероятнейшее число k₀ попада­ний в мишень при семи выстрелах.

Решение. Рассматриваемый в задаче эксперимент удовлетворяет схеме Бернулли. Пусть A – собы­тие «Попадание в мишень при вы­стреле». Тогда событие`A означает «промах». По условию P(A) = p = 0,8, значит, P(`A) = q = 1 – p = 0,2.

а) Для нахождения пяти попаданий при семи выстрелах воспользу­емся теоремой 2.10.: P₇(5) = С₇⁵·p⁵·q^7-5 = » 0,275.

б) Наивероятнейшее число попаданий в мишень при семи выстре­лах находим (согласно теоремы 2.11) из двойного неравенства 7·0,8-0,2 £ k₀ £ 7·0,8+0,8, т.е. 5,4 £ k₀ £ 6,4. Значит, k₀ = 6.

Ответ: а) » 0,275; 6.

▲Теорема 2.12. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события A равна p, а не появления – q. Тогда вероятность со­бытия, заключающегося в том, что при n испытаниях событие A появится не менее k₁ и не более k₂ раз, вычисляется по формуле: P_n(k₁£ k £k₂) = С_n^mp^mq^n-m.

Пример 2.19. Вероятность заболевания гриппом во время эпидемии равна 0,4. Найти вероятность того, что из 8 учеников класса заболеют не менее трех и не более шести учеников.

Решение. Рассматриваемый в задаче сюжет удовлетворяет схеме Бернулли, где p=0,4, q=1-p =0,6, n=8, k₁=3, k₂=6, поэтому P_n(3£ k £5) = С₈³p³q^8-3 + С₈⁴p⁴q^8-4 + С₈⁵p⁵q^8-5 + С₈⁶p⁶q^8-5 = ++ ++ 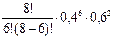» 0,676.

Ответ: » 0,676.

В некоторых случаях возникает потребность вычисления ве­роятностей P_n(k) для весьма больших n и k, что сложно сделать с помощью формулы Бернулли. В этом случае используют при­ближенные формулы.

▲Теорема 2.13. Пусть производится n независимых испытаний, в каждом из которых вероятность появления события A равна p, а непоявления – q. Тогда вероятность P_n(k) того, что в n испы­таниях при достаточно большом n и малом p (например, n>100 и a=np<10) событие A появится ровно k раз, вычисляется по фор­муле Пуассона:

 

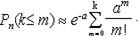Вероятность события, заключающегося в том, что A поя­вится не более m раз, вы­чис­ляется по формуле

 

 

Для облегчения проведения расчетов формулы Пуассона табулированы (см. таб­лицы 1 и 2 Приложения).

Пример 2.20. Известно, что 2,5% учащихся школы освобождены от занятий физкультурой. Найти ве­роятность того, что среди 200 школь­ников освобожденными от физкультуры окажется: а) ровно 4 ученика; б) не более 6 учеников.

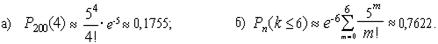Решение. Поскольку вероятность p=0,025 мала, n>100 и a = np = 5 < 10, то воспользовавшись фор­му­лами Пуассона и данными таблиц 1 и 2 Приложения, будем иметь:

 

 

Ответ: а) 0,1755; б) 0,7622.

При достаточно большом n и не слишком больших p и q фор­мула Пуассона дает зна­чительную погрешность, поэтому при­меняется другое приближение – формула Му­авра-Лапласа.

▲Теорема 2.14. (Локальная теорема Лапласа). Если вероят­ность p появления собы­тия A в каждом испытании постоянна и отлична от нуля и единицы, то вероятность того, что событие A появится в n испытаниях ровно k раз, приближенно равна

.

 

Значение функции j(x) помещены в таблице 3 Приложе­ния (в силу четности функ­ции, таблица ее значений состав­лена при x³0).

Пример 2.21. Найти вероятность того, что событие А наступит ровно 80 раз в 400 испыта­ниях, если вероятность появления этого со­бытия в каждом испытании равна 0.2.

Решение. По условию n=400; k=80; p=0,2; q=0,8. Воспользуемся ло­кальной теоремой Лапласа: P₄₀₀(80) » · j(x) = ·j(x) . Вычислим определяемое данными задачи значение х: x = = 0. По таблице 3 Приложения находим j (0) = 0,3989. Значит, искомая вероятность P₄₀₀(80) » · 0,3989 = 0,04986.

Ответ: 0,04986.

▲Теорема 2.15. (Интегральная теорема Лапласа). Пусть производится n независи­мых испытаний, в каждом из кото­рых вероятность появления события A равна p, а непо­явле­ния – q. Тогда вероятность события, заключающегося в том, что при n испы­та­ниях событие A появится не менее k₁ и не более k₂ раз, равна

P_n(k₁£ k £k₂) » Ф(x₂) – Ф(x₁),

где

Функция Ф(x) называется функцией Лапласа. Эта функ­ция нечетная (Ф(-x) = -Ф(x)), ее значения для 0£x<5 пред­ставлены в таблице 4 Приложения (для x³5 Ф(x) » 0,5).

Пример 2.22. Вероятность того, что абитуриенты, получившие об­разование в лицее, поступают в вузы равна 0,8. Какова вероятность того, что из 100 абитуриентов-лицеистов не менее 75 поступят в вузы.

Решение. Учитывая, что n = 100 велико, p=0,8 и q=0,2 не малы, воспользуемся интегральной тео­ре­мой Лапласа

P₁₀₀(75£ k £100) » Ф(x₂) – Ф(x₁) = =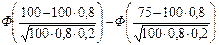

= Ф(5) – Ф(-1,2) = Ф(5)+Ф(1,2) =0,5+0,385 = 0,885.

 

Шифратор – схема, имеющая 2ⁿ входов и n выходов, функции которой во многом противоположны функции дешифратора (рис. 1.4). Эта комбинационная схема в соответствии с унитарным кодом на своих входах формирует позиционный код на выходе (таблица 1.2).

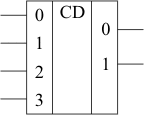
Рис. 1.4. Условно-графическое обозначение шифратора на 4 входа