Плотность распределения вероятностей

Функция распределения для непрерывной случайной величины является ее исчерпывающей вероятностной
характеристикой, но она имеет недостаток, так как по ней трудно судить о характере распределения случайной
величины в небольшой окрестности той или иной точки числовой оси. Более наглядное представление о
характере распределения непрерывной случайной величины в окрестностях различных точек дает функция,
которая называется плотностью распределения вероятностей и обозначается .

(4)

Плотность распределения - это средняя вероятность, которая приходится на единицу длины промежутка .
Она указывает на то, как часто случайная величина появляется в некоторой окрестности точки при
повторении испытаний. Эту функцию еще называют дифференциальным законом распределения.
На рис.4 дан примерный вид функции .

Рис.4

График функции называется кривой распределения.

Так как , то

(5)

Свойства плотности распределения

1. ;
2. .
Геометрически это означает, что площадь под кривой распределения равна 1.

Функция распределения и плотность распределения связаны еще одним соотношением:

(6)

Вероятность того, что случайная величина примет значение из промежутка , можно
вычислить с помощью плотности распределения по формуле:

(7)

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение из
промежутка , равна площади криволинейной трапеции с основанием (рис.5).

Рис.5

 

Пример 8.Дана плотность распределения вероятностей непрерывной случайной величины :

Найти , построить график функции , найти .
Решение.Для нахождения коэффициента воспользуемся свойством 2 плотности распределения, тогда

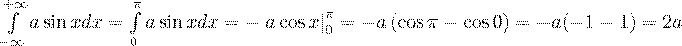, получаем, что ,
следовательно, .

Теперь построим график плотности распределения:

Рис.6

Требуемую вероятность вычисляем по формуле (7):

.

Вопрос.Для каких случайных величин закон распределения задается с помощью плотности распределения?

 

Ваш ответ