Теоремы сложения вероятностей

Теорема 1.Если события A и B несовместны, то

(11)

 

Теорема 2.Если - группа несовместных событий, то

(12)

 

Теорема 3.Если события образуют полную группу несовместных событий,то

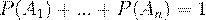(13)

Теорема 4.Так как противоположные события образуют полную группу несовместных событий, то

(14)

Пример 23.Проверяется партия из 80 деталей, среди которых 6 бракованных, для этого наудачу
берется 40 деталей. Найти вероятность того, что партия будет принята, если условия приема
допускают не более двух бракованных деталей среди проверенных.
Решение.Пусть A={ среди проверенных деталей 0 бракованных}, B={среди проверенных деталей
1 бракованная}, C={среди проверенных деталей 2 бракованных},D={партия деталей будет принята}.
Тогда , так как события несовместны, то .
Найдем вероятность каждого события, используя классическое определение вероятности. В данном случае
испытание - это выбор 40 деталей из 80, тогда всего исходов, соответствующих данному испытанию
, теперь вычислим число исходов, благоприятствующих каждому
событию: ; ; 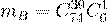, получаем

Теорема 5.Если события A и B совместны, то

(15)

 

Теорема 6.Если события A,B,C образуют группу совместных событий, то

(16)

Пример 24.В коробке 3 шара, занумерованных числами 1,2,3. Шары извлекают по одному без возвращения.
Найти вероятность того, что хотя бы один раз номер шара совпадет с порядковым номером его извлечения.
Решение. Пусть A_i={шар с номером i извлечен i-ым по порядку},i=1,2,3; A={хотя бы один раз номер шара
совпадет с порядковым номером его извлечения}, тогда A=A₁+A₂+A₃. Так как события A_i совместны, то
вероятность A будем вычислять по формуле (16). 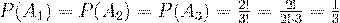, теперь
и ; окончательно получаем
.

Вопрос. , тогда равна

0,25

0,75

0,5

 

 

Теоремы умножения вероятностей

Теорема 7.Данная теорема является обобщением аксиомы 5.

(17)

Пример 25.В урне 6 белых и 14 черных шаров. Наудачу поочереди вынимают( без возврата) 3 шара. Найти
вероятность того, что все они черные.
Решение.Пусть ={первый извлеченный шар черный}, ={второй извлеченный шар черный}, =
{третий извлеченный шар черный},={все извлеченные шары черные}. Тогда и вероятность
события будем вычислять по формуле (17): .

Определение 26.Два события называются независимыми, если вероятность одного из них не меняется от того,
произошло другое или нет:

 

(18)

или

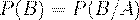(19)

Теорема 8.Если события и являются независимыми , то

(20)

Определение 27.События называются независимыми в совокупности,если вероятность каждого
из них не меняется от того, произойдут или нет другие события ( одно или несколько в любой комбинации и в
любом количестве).

Теорема 9.Если события являются независимыми в совокупности, то

(21)

Пример 26.Рассмотрим условия примера 25, но шары извлекаются с возвратом. Найти вероятность того, что
все шары будут черными.
Решение.Так как шары извлекаются с возвратом, то события, определенные в примере 25, будут
независимыми, поэтому для вычисления вероятности того, что все извлеченные шары будут черными воспользуемся формулой (21):
.

Пример 27.Вероятность попадания в мишень при одном выстреле равна 0,7. Найти вероятность хотя бы одного
попадания при трех выстрелах.
Решение.Пусть ={попадание при i-ом выстреле}, 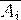={промах при i-ом выстреле},где i=1,2,3;={хотя бы одно попадание при трех выстрелах}, ={ни одного попадания при трех выстрелах}.
.
Проще вычислить вероятность противоположного события, то есть события . Так как
, а эти события независимы, то
,
теперь получаем .

Вопрос.События и независимые. .Тогда вероятность события равна

 

0,48

0,08

0,2

1,4