Форматы представления данных

Любая информация (числа, команды, алфавитно-цифровые записи и т. п.) представляется в компьютере в виде двоичных кодов. Отдельные элементы двоичного кода, принимающие значения 0 или 1, называются разрядами или битами.

В старых компьютерах, рассчитанных на вычислительные задачи, минимальной единицей информации, доступной для обработки, была ячейка. Количество разрядов в ячейке было ориентировано на представление чисел и было различным в разных компьютерах (24 бита, 48 бит и т.д.). Однако такой большой размер ячеек был неудобен для представления символов, поскольку для представления символьных данных достаточно 5-8 байт. Это дает возможность представить от 32 до 256 символов.

Поэтому минимальной единицей данных, обрабатываемой в современном компьютере, является байт, состоящий из восьми двоичных разрядов (битов). Байт впервые был введен в компьютерах серии IBM/360 и используется для представления как чисел, так и символов. Каждый байт, расположенный в памяти компьютера, имеет свой адрес, который определяет его местонахождение и задается соответствующим кодом. Адреса памяти начинаются с нуля для первого байта и последовательно возрастают на единицу для каждого последующего.

Производными единицами от байта являются килобайт (2¹⁰ байт) – сокращение Кбайт или Кб, мегабайт (2²⁰ байт) – сокращение Мбайт или Мб, гигабайт (2³⁰ байт) – сокращение Гбайт или Гб, терабайт (2⁴⁰ байт) – сокращение Тбайт или Тб и петабайт (2⁵⁰ байт) – сокращение Пбайт или Пб.

Для представления чисел используются один или несколько последовательно расположенных байтов. Группы байтов образуют двоичные слова, которые, в свою очередь, могут быть как фиксированной, так и переменной длины.

Форматы данных фиксированной длины (полуслово, слово и двойное слово) состоят соответственно из одного, двух или четырех последовательно расположенных байтов. Обращение к этим данным производится по адресу крайнего левого байта формата, который для слова должен быть кратен числу 2, а для двойного слова – числу 4.

Формат данных переменной длины состоит из группы последовательно расположенных байтов от 1 до 256. Адресация таких данных производится, как и в форматах фиксированной длины, по адресу самого левого байта.

В зависимости от характера информации используются форматы представления данных как фиксированной, так и переменной длины. Так, в форматах данных фиксированной длины обычно представляются двоичные числа, команды и некоторые логические данные, а в форматах данных переменной длины – десятичные числа, алфавитно-цифровая и некоторая логическая информация.

В современных компьютерах применяются две формы представления чисел: с фиксированной точкой (запятой) и с плавающей точкой (запятой). Эти формы, кроме того, называются соответственно естественной и полулогарифмической.

При представлении чисел с фиксированной точкой положение точки фиксируется в определенном месте относительно разрядов числа. В первых компьютерах точка фиксировалась перед старшим разрядом числа, поэтому представленные числа по абсолютной величине были меньше единицы. В современных компьютерах точку фиксируют справа от самого младшего разряда и поэтому могут быть представлены только целые числа. При этом используются два варианта представления целых чисел: со знаком и без знака.

Для числа со знаком крайний слева разряд отводится под знак числа. В этом разряде записывается нуль для положительных чисел и единица – для отрицательных чисел. Числа без знака занимают все разряды числа, т.е. числа могут быть только положительными. Нумерация разрядов числа обычно ведется справа налево.

В компьютерах числа с фиксированной точкой имеют три основных формата – один байт (полуслово), 16-разрядное слово (короткий формат) и 32-разрядное двойное слово (длинный формат).

На рис. 1.2.7 приведены форматы представления чисел с фиксированной точкой со знаком (1.2.7а) и без знака (1.2.7б) длиной в полуслово (числа короткого и длинного формата имеют аналогичной представление).

Рис. 1.2.7. Представление числа с фиксированной точкой длиной в полуслово:

а) со знаком; б) без знака

 

Следует отметить, что интерпретацию числа с фиксированной точкой как числа со знаком или без знака должна выполнять программа обработки этих чисел. Так, число 01110011₂ = 73₁₆ будет иметь десятичное значение 115₁₀ и как число со знаком и как число без знака. Однако число 11101101₂ = ED₁₆ будет иметь десятичное значение -109₁₀ как число со знаком и 237₁₀ – как число без знака.

Диапазон изменения чисел X c фиксированной точкой со знаком составляет:

-2^n-1 £ X £ 2^n-1 - 1,

а чисел без знака:

0 £ X £ 2ⁿ - 1.

где n – разрядность числа. Так, для n=8 диапазон изменения чисел со знаком – от -128₁₀ до +127₁₀, а чисел без знака – от 0₁₀ до 255₁₀.

Для представления чисел, не укладывающихся в диапазон двойного слова, в современных компьютерах можно использовать два варианта:

· введение и обработка чисел произвольной длины (например, 8 или 10 байт);

· использование масштабных коэффициентов.

И в том, и в другом варианте время выполнения операций над числами существенно увеличиваются (в первом варианте из-за большой длины числа, во втором – из-за необходимости вручную отслеживать положение десятичной точки в числе).

Другим недостатком является то, что для представления чисел с фиксированной точкой относительная точность выполняемых расчетов зависит от величины чисел и является максимальной при выполнении операций с максимально возможными числами.

В связи с этим, наряду с представлением чисел с фиксированной точкой, в современных компьютерах используется также форма представления чисел с плавающей точкой.

Любое число N, представляемое в форме с плавающей точкой, является произведением двух сомножителей:

N = mS^p,

где m – мантисса числа N (|m| < 1), S – основание системы счисления; р – целочисленный порядок. С изменением порядка в ту или иную сторону точка как бы «плавает» в изображении числа

Примером записи десятичного числа в форме с плавающей точкой является так называемая экспоненциальная форма записи, например:

0,35×10¹² или -0,1563×10^-12.

Следовательно, при представлении чисел с плавающей точкой необходимо записать в компьютер со своими знаками мантиссу m и порядок р. И мантисса и порядок записываются в двоичном виде, т.е. со значением S =2. Знак числа при этом совпадает со знаком мантиссы.

Чтобы упростить операции над порядками, их сводят к действиям над целыми положительными числами путем использования так называемого смещенного порядка, который всегда положителен. Смещенный порядок p_см образуется прибавлением к порядку р числа 2ⁿ⁺¹ (где n – количество бит , отводимое под порядок). Например, для n=7 p_см = p + 64 порядок будет принимать значения от 0 (при p = -64) до 127 (при p = 63). В этом случае, если p = -15, смещенный порядок будет равен: p_см = -15 + 64 = 49.

Число разрядов, выделенных для изображения порядков, определяет диапазон представимых в компьютере чисел с плавающей точкой. Кроме того, большое значение имеет точность представления чисел, которая повышается с увеличением числа разрядов мантиссы.

Поэтому с учетом различных требований, предъявляемых к точности решения задач, в компьютерах обычно используются несколько форматов. В компьютерах типа IBM PC для представления значений с плавающей точкой используется стандартный формат IEEE (Institute of Electrical and Electronics Engineers), определяющий три формы задания чисел: обычный, двойной точности и длинный.

Обычный формат занимает двойное слово (32 бита), состоящее: из бита знака, 7-битового двоичного порядка и 24-битовой мантиссы, представляющей число в диапазоне от 1.0 до 2.0 (рис. 1.2.8). Поскольку старший бит мантиссы всегда равен 1, он не хранится в памяти. Это представление дает 7 значащих цифр и область значений приблизительно от 3.4·10^-38 до 3.4·10⁺³⁸.

Рис. 1.2.8. Представление числа с плавающей точкой обычного формата

 

Формат двойной точности занимает двойное слово (64 бита). Этот формат аналогичен короткому формату, за исключением того, что порядок занимает 11 бит, а мантисса – 52 бита (плюс неявный старший единичный бит). Это представление дает 15 значащих цифр и область значений приблизительно от 1.7·10^-308 до 1.7·10⁺³⁰⁸.

Длинный формат занимает 10 байт (80 бит). Его представление аналогично представлению чисел с двойной точности, за исключение того, что мантисса занимает 68 бит. Количество значащих цифр для этого формата – 19, а диапазон значений – приблизительно от 3.4·10^-4932 до 1.1·10⁺⁴⁹³².

Третья форма представления чисел в компьютерах – это двоично-десятичная форма. В этой форме каждая цифра десятичного числа хранится в четырех битах, т.е. две цифры на байт. Цифры от 0 до 9 представлены двоичными кодами от 0000 до 1001. Двоичные значения 1100 и 1101 используются соответственно для знака "+" и знака "-". Положение десятичной точки в этом случае фиксируется и отслеживается программными средствами. Пример: -142₁₀ = 1101 0001 0100 0010. Для этой формы представления чисел, так же, как и для чисел с фиксированной и плавающей точкой, определены арифметические операции. Однако данная форма представления чисел в настоящее время используется крайне редко, в основном, при обработке больших массивов десятичных чисел.

Для упрощения арифметических операций числа в компьютере представляются специальными кодами – прямым, обратным и дополнительным. При помощи этих кодов операция вычитания (или алгебраического сложения) сводится к арифметическому сложению, упрощается определение знака результата операции, а также облегчается выработка признаков переполнения результата (когда в результате арифметических операций число становится больше максимально допустимого для данной формы значения).

Прямой код двоичного числа содержит цифровые разряды, слева от которых записывается знаковый разряд. Сложение в прямом коде чисел, имеющих одинаковые знаки, выполняется достаточно просто. Цифровые разряды чисел складываются по правилам арифметики и сумме присваивается код знака слагаемых. Значительно сложнее реализуется в прямом коде операция алгебраического сложения, т. е. сложения чисел, имеющих разные знаки. В этом случае приходится определять большее по модулю число, производить вычитание чисел и присваивать разности знак большего по модулю числа.

Данная операция сводится к простому арифметическому сложению при помощи обратного или дополнительного кода, которыми представляются отрицательные числа.

Обратный код отрицательного числа получается по следующему правилу: в знаковый разряд числа записывается единица, в цифровых разрядах нули заменяются единицами, а единицы – нулями.

Дополнительный код отрицательного числа получается из обратного кода путем прибавления единицы к младшему разряду.

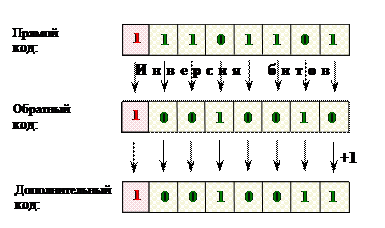Представление отрицательного числа -109₁₀ в прямом коде и его преобразование в обратный и дополнительный код показано на рис. 1.2.9.

 

Рис. 1.2.9. Представление отрицательного числа в прямом,

обратном и дополнительном кодах

 

При использовании обратного или дополнительного кода операция алгебраического сложения сводится к простому арифметическому сложению. При этом положительные числа представляются в прямом коде, а отрицательные – в обратном или дополнительном коде. Затем производится арифметическое суммирование этих кодов, включая знаковые разряды, которые при этом рассматриваются как старшие. При использовании обратного кода возникающая единица переноса из знакового разряда циклически прибавляется к младшему разряду суммы кодов, а при использовании дополнительного кода эта единица отбрасывается.

Как уже говорилось, компьютеры могут обрабатывать только информацию, представленную в числовой форме. При вводе документов, текстов программ и т.д. вводимые буквы кодируются определенными числами, а при выводе их для чтения человеком (на монитор, принтер и т.д.) по каждому числу (коду символа) строится изображение символа. Соответствие между набором символов и их кодами, как уже говорилось, называется кодировкой символов.

Как правило, код символа хранится в одном байте. Код символа рассматривается как число без знака и, следовательно, может принимать значения в диапазоне от 0 до 255. Такие кодировки называются однобайтными, они позволяют использовать до 256 различных символов. В настоящее время все большее распространение получает двухбайтовая кодировка Unicode, в которой коды символов могут принимать значения от 1 до 65535. В этой кодировке имеются номера для практически всех применяемых символов (буквы и иероглифы различных языков, математические, декоративные символы и т.д.).

Кодировка символов, как правило, определяется используемой операционной системой или программной оболочкой, поэтому кодировки, используемые в MS DOS и Windows, будут рассмотрены при изучении этих систем.

В целом, наличие в современных компьютерах различных форм и форматов представления чисел позволяет выбирать те из них, которые в наибольшей степени отвечают требованиям решаемых задач.