III. Статистические характеристики ряда динамики

При изучении динамики социально-экономических явлений используют некоторые статистические характеристики (показатели), которые позволяют измерить изменение явлений во времени.

Большинство статистических характеристик основано на абсолютном или относительном сравнении уровней динамических рядов. К показателям динамики относятся: абсолютный прирост, темпы роста и прироста, абсолютное значение одного % прироста.

Символика обозначений уровней ряда динамики:

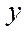- каждый показатель ряда динамики называется уровнем;

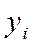- уровень изучаемого i-го периода;

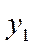- начальный уровень;

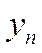- конечный уровень;

- уровень, предшествующий изучаемому периоду;

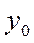- базисный уровень;

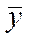- средний уровень.

 

1) Абсолютный прирост - называется разность последующего и предыдущего уровней ряда динамики:

где - текущий уровень ряда динамики;

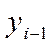- предыдущий уровень;

- абсолютный прирост.

За весь период, абсолютный прирост выразится как разность между последним уровнем ряда и первым его уровнем:

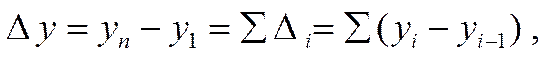
где 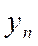- последний уровень ряда;

- первый уровень.

Абсолютный прирост может иметь положительный или отрицательный знак. Он показывает, насколько уровень текущего периода выше или ниже базисного.

Абсолютный прирост определяется на базисной и цепной основе.

При определении накопленных (базисных) абсолютных приростов за базу сравнения принимается постоянный уровень и расчет производится по формуле:

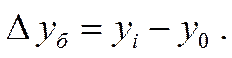
При определении цепных абсолютных приростов базой сравнения каждый раз выступает уровень предыдущего периода, и расчет абсолютных приростов производится по формуле:

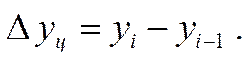
Между базисными и цепными абсолютными приростами имеется связь: сумма цепных абсолютных приростов 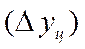равна базисному абсолютному приросту последнего периода ряда динамики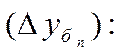

.

 

Пример. Производство часов наручных характеризуется следующими данными:

Год	Выпуск часов наручных, млн.шт.
	21,7 31,3 33,3 35,3 37,0 38,5 40,37

Определите: абсолютные приросты (по годам и к базисному 1998г.):

 

 

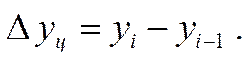
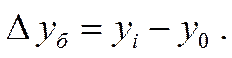
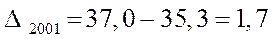
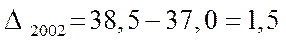
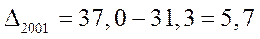
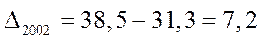
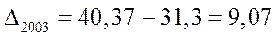
2) Темп роста : называется отношение данного уровня явления к предыдущему или начальному, выраженное в %. Если темп роста выражен в коэффициентах, то он называется коэффициентом роста.

Темпы роста, исчисленные как отношение данного уровня к предыдущему, называются цепными, а к начальному – базисными:

или

где 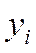- текущий уровень ряда;

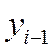- уровень, предшествующий;

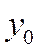- базисный уровень.

 

Пример 2. определите темпы роста производства часов наручных

а)- по годам, и б)- к базисному 1998г.

 

а)

1999г. 33,3 : 31,3 = 1,0639 или 106,39 %

2001г. 35,3 : 33,3 = 1,06006 или 106,006 %

2001г. 37,0 : 35,3 = 1,04815 или 104,815 %

2002г. 38,5 : 37,0 = 1,04054 или 104,054 %

2003г. 40,37:38,5 = 1,04857 или 104,857 %

 

б)

1999г. 33,3 : 31,3 = 1,0639 или 106,39 %

2000г. 35,3 : 31,3 = 1,1278 или 112,78 %

2001г. 37,0 : 31,3 = 1,1821 или 118,21 %

2002г. 38,5 : 31,3 = 1,23003 или 123,003 %

2003г. 40,37:31,3 = 1,2898 или 128,98 %.

 

Между базисными и цепными темпами роста имеется взаимосвязь: произведение последовательных цепных темпов роста равно базисному темпу роста, а частное от деления последующего базисного темпа роста на предыдущий равно соответствующему цепному темпу роста:

 

 

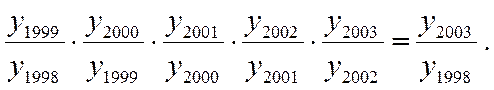
3). Темп прироста 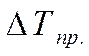- называется отношение абсолютного прироста к предыдущему или базисному уровню, выраженное в %.

 

или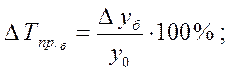

 

Если при определении темпов прироста DТ предварительно были исчислены темпы роста Тр, то расчет темпов прироста производят так:

 

DTпр = Тр - 1; или DTпр = Тр - 100%,

если темп роста выражен в %.

 

 

Пример: определите темп прироста -

а) по годам, и б) к базисному 1998 году).

 

Годы

 

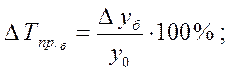
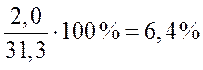
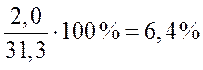
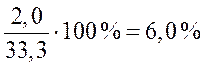
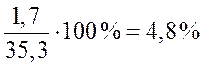
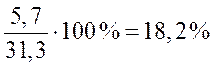
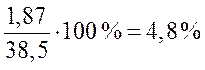
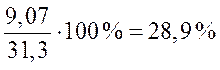
Важным статистическим показателем является темп наращивания,который в условиях интенсификации экономики измеряет наращивание во времени экономического потерциала. Вычисляются темпы наращивания 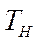делением цепных абсолютных приростов на уровень , принятый за постоянную базу сравнения :

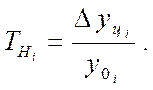
Темпы наращивания можно непосредственно определять по базисным темпам роста:

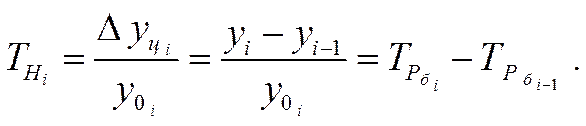
4). Абсолютное значение одного % прироста (А%) показывает, какая абсолютная величина скрывается за относительным показателем - одним процентом прироста.

Показатель абсолютного значения одного % прироста (А%) определяется путем отношения (в каждом периоде) абсолютного прироста D yц к темпу прироста DTпр ц. Расчет этого показателя имеет экономический смысл только на цепной основе:

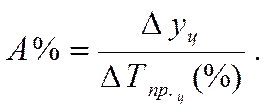
Пример. Рассчитать уровень абсолютного значения одного процента прироста.

1999г. ;

2000г. ;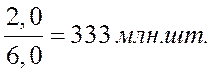

2001г. ;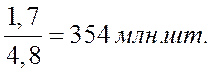

2002г. ;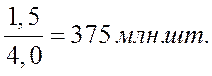

2003г. .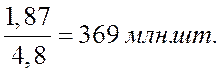

При анализе погодовых уровней ряда динамики расчет абсолютного значения 1% прироста можно произвести по схеме:

А% = 0,01 уi-1.

IV. СРЕДНИЕ ПОКАЗАТЕЛИ