Обращение суждений

Превращение суждений,

противопоставление предикату.

Превращение суждений (лат. – obversio)

Смысл превращения состоит в том, что мы выявляем в утвердительном суждении отношения различия, а в отрицательном – отношение тождества, содержащиеся в суждениях в неявной форме.

Формально операция превращения состоит в том, что мы изменяем связку исходного суждения на противоположную и заменяем его предикат противоречащим понятием. Например:

 

Схема превращения: (Ѕ есть Р)

( Ѕ не есть не-Р)

Обращение суждений (лат. – conversio)

Обращение есть непосредственное суждение о предикате данного суждения.

Все студенты – умники → некоторые умники есть студенты

Обращение подчиняется следующему правилу: термин, не распределенный в исходном суждении, не может быть распределен в новом, выводном суждении.

 

Схема обращения: Ѕ есть Р

некоторые Р есть Ѕ

Противопоставление предикату (лат. – opposition praedicati) ‑ это умозаключение, состоящее из соединения превращения с обращением.

	Все металлы – химические элементы Ни один не химический элемент не есть металл

 

Схема противопоставления предикату : Ѕ есть Р

не Р не есть Ѕ

Противопоставление предикату можно получить, применяя последовательно операции сначала превращения, а затем обращения. Например, превращаем суждение «все металлы электропроводны», получаем суждение « ни один металл не есть неэлектропроводен». Обращая это суждение, получаем суждение «ни одно неэлектропроводное тело не есть металл».

Теперь отвлекитесь от чтения и попробуйте разобраться самостоятельно в ошибочном выводе из следующего умозаключения:

«некоторые гениальные люди не принесли обществу никакой пользы; следовательно, между вредными для общества людьми оказывались иногда гениальные личности».

 

Умозаключение, в котором происходит переход от знания меньшей степени общности к знанию большей степени общности называется индуктивным (лат. induction − наведение).

Индуктивные умозаключения

Разница между дедукцией и индукцией

· дедукция бывает лишь изредка обобщающим умозаключением

· индукция является только обобщающим умозаключением.

· дедукция доказывает обобщение независимо от этих принципов, и вывод делает только на основе установленных правил.

· В индукции основой вывода является принцип причинно-следственной связи

· в дедукции заключение следует из посылок с необходимостью

· в индукции вывод следует с вероятностью, приближающейся либо к нулю, либо к единице

 

 

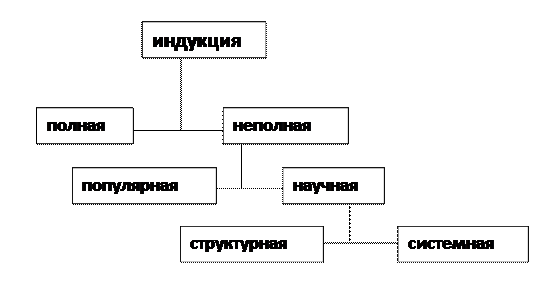
только в полной индукции, когда определены все предметы данного класса и выбранный признак является общим и существенным для этого класса, вероятность достоверности вывода равна единице.

 

 

Схема полной индукции:

Ѕ1 − Р

Ѕ2 − Р

…….

Ѕn − Р

Ѕ1^ Ѕ2^….. Ѕn есть все предметы класса А

А есть Р

 

Схема неполной индукции:

Ѕ1 − Р

Ѕ2 − Р

…….

Ѕn − Р

Ѕ1^ Ѕ2^….. Ѕn есть часть предметов класса А

вероятно, А есть Р

	Индукция через простое перечисление, где не встречается противоречащих случаев, называется популярной.
	Индукция, основанная на обобщении существенных и необходимых признаков у части предметов данного множества и делается вывод об их принадлежности всему множеству называется научной.

 

 

Схема научной индукции:

Ѕ1 имеет необходимый и существенный признак Р

Ѕ2 имеет необходимый и существенный признак Р

…….

Ѕn имеет необходимый и существенный признак Р

…….

 

Ѕ1^ Ѕ2^….. Ѕn есть часть предметов класса А

вероятно, А есть Р

 

В системной индукции используется метод отбора. Отобранные предметы и явления с существенными признаками составляют систему исследуемого объекта.

В зависимости от методов, которые используются в научной индукции она делится на системную и структурную.

 

	В структурной индукции используется метод исключения, который устанавливает причинно-следственную связь предметов и явлений на основании предшествующих им событий и исключении не относящихся к ним обстоятельств.

 

 

Методы установления причинной связи явлений.

	Причиной называется явление вызывающее другое явление. Вызванное явление называется следствием.

 

В логике имеется пять методов установления причинной связи:

Методы Милля

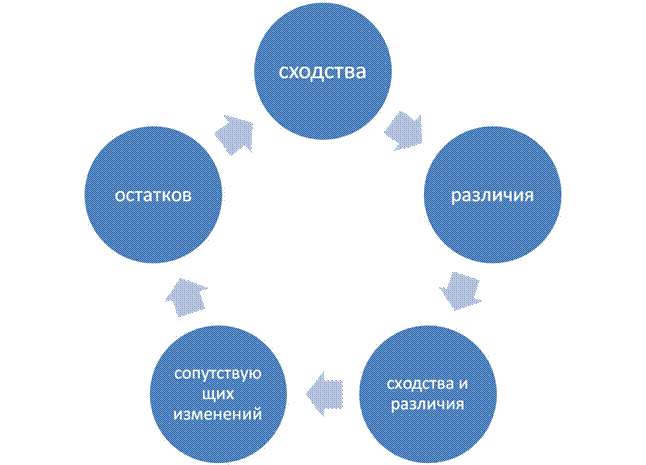
1) метод сходства

Если два или более случаев наступления наблюдаемого явления сходны только в одном предшествующем обстоятельстве, то вероятно это обстоятельство и является причиной данного явления:

АВС – а

АКМ – а

вероятно, А есть причина а

 

2) метод различия

если случай, в котором исследуемое явление наступает, и случай, в котором оно не наступает совпадают во всех обстоятельствах. кроме одного, встречающегося только в первом случае, то эта единственная разница и есть следствие, или причина (или необходимая часть причины) явления:

АВС ‑ а

- ВС -

вероятно, А есть причина а