Первоначальные сведения о граничной задаче.
Решить уравнение  (1), здесь
(1), здесь  , при условии
, при условии
 (2).
(2).
Функции a(t), b(t) и f(t) – определены и непрерывны на отрезке  .
.
 - постоянные.
- постоянные.
Условия (2) называются краевыми или граничными условиями, а сама задача (1),(2) – краевой задачей. Для краевой задачи (1),(2) может иметь место любой из трёх возможных вариантов решений:
- Задача имеет единственное решение.
- Решение не существует.
- Существует бесконечное множество решений.
Пример.  ,
,  - общее решение.
- общее решение.
Рассмотрим следующие три краевые задачи с граничными условиями:
1.  .
.
2.  .
.
3.  .
.
В случае 1. имеем единственное решение  ;
;  .
.
В случае 2. решения нет.
В случае 3. бесконечное число решений  .
.
Рассмотрим два способа решения задачи (1),(2), причём будем предполагать, что решение этой задачи существует и единственно.
Ι. Метод “стрельбы”.
Пусть  - частное решение уравнения (1), удовлетворяющее начальным условиям
- частное решение уравнения (1), удовлетворяющее начальным условиям

 (3).
(3).
 - произвольное число, а y0(t) – решение соответствующего однородного уравнения
- произвольное число, а y0(t) – решение соответствующего однородного уравнения  (4), удовлетворяющее начальным условиям
(4), удовлетворяющее начальным условиям  ,
,  ,
,  - произвольное число.
- произвольное число.
Тогда при любом с функция  (5) - решение уравнения (1), удовлетворяющее первому из условий (2).
(5) - решение уравнения (1), удовлетворяющее первому из условий (2).
Число с выбираем так, чтобы (5) удовлетворяло второму из условий (2).

 (6).
(6).
 , ибо в противном случае краевая задача (1),(2) либо не имеет решения, либо имеет бесконечное множество решений.
, ибо в противном случае краевая задача (1),(2) либо не имеет решения, либо имеет бесконечное множество решений.
При численном решении краевой задачи метод “стрельбы” имеет существенный недостаток. Ошибка вычисления решения x(t):  может быть очень большой за счёт слагаемого
может быть очень большой за счёт слагаемого  .
.
ΙΙ. Решение однородной краевой задачи с помощью функции Грина.
 (1),
(1),
 (7), где
(7), где  .
.
Будем предполагать, что рассматриваемая краевая задача имеет единственное решение.
Пусть x = x1(t) – ненулевое решение однородного уравнения 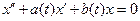 , удовлетворяющее первому из условий (7), а x2(t) – ненулевое решение, удовлетворяющее второму условию (7). Причём x1(t) и x2(t) линейно независимые решения. Тогда
, удовлетворяющее первому из условий (7), а x2(t) – ненулевое решение, удовлетворяющее второму условию (7). Причём x1(t) и x2(t) линейно независимые решения. Тогда
 (8).
(8).
Решение уравнения (1) будем искать методом вариации произвольных постоянных.
 (9).
(9).
Для определения функций 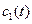 и
и  получим следующую систему:
получим следующую систему:
 (10).
(10).
Решая систему (10), получим  (11), где
(11), где 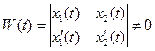 . Интегрируя (11), получим:
. Интегрируя (11), получим:
 , где
, где 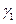 и
и  - постоянные.
- постоянные.
 (12).
(12).
Продифференцируем (12) по t, получим  (13).
(13).
Потребуем, чтобы (12) удовлетворяло первому из условий (7), получим  =0. Аналогично, подставляя (12) во второе условие (7), получим
=0. Аналогично, подставляя (12) во второе условие (7), получим  =0.
=0.
Итак,  (14) или
(14) или  (15),
(15),
где  или
или  (16)
(16)
построенная функция G(t,s) называется функцией Грина краевой задачи. Сама функция Грина от f(t) не зависит.
Функция Грина обладает следующими свойствами:
1) при 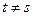 : G(t,s) удовлетворяет однородному уравнению
: G(t,s) удовлетворяет однородному уравнению 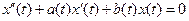
2) при t=t0 и t=t1: G(t,s) удовлетворяет соответственно первому и второму граничным условиям
3) при t=s: G(t,s) – непрерывна
4) при t=s: производная  имеет скачёк, равный 1:
имеет скачёк, равный 1: 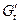 │
│ ─
─ 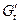 │
│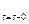 =1.
=1.
Свойства 1-3 просто проверяются подстановкой. Докажем свойство 4.
 ;
; 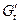 │
│ ─
─ 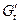 │
│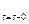 =
= =1.
=1.
Построим функцию Грина для краевой задачи 
 .
.
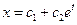 - общее решение однородного уравнения
- общее решение однородного уравнения 
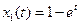 - удовлетворяет первому граничному условию.
- удовлетворяет первому граничному условию.
 - удовлетворяет второму граничному условию.
- удовлетворяет второму граничному условию.

Глава 2: Линейные системы дифференциальных уравнений.
ЛЕКЦИЯ 8:
Системы вида  ,
,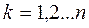 называются линейными.
называются линейными.
Будем предполагать, что 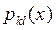 ,
,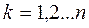 и
и  непрерывны в интервале
непрерывны в интервале 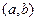 . Согласно теореме Пикара система имеет единственное решение
. Согласно теореме Пикара система имеет единственное решение  ,
, 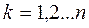 удовлетворяет начальным условиям
удовлетворяет начальным условиям  при
при  ,
, 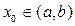 ,
,  произвольные.
произвольные.
Решение определено в интервале 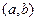
Особых решений линейная система (1) не имеет.
Если 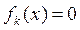 ,
,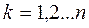 , то система (1) называется однородной
, то система (1) называется однородной 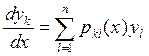 ,
, 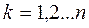 (2)
(2)
