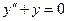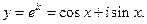Введение.

Глава 1. Линейные дифференциальные уравнения n-го порядка.

ЛЕКЦИИ 1-2.

Линейные уравнения – это наиболее разработанная часть теории диф. уравнений, так как они либо описывают реальные процессы, либо дают первое приближение и во многих случаях по этому приближению можно судить о характере изучаемого явления.

Линейным дифференциальным уравнением называется уравнение вида

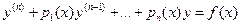, (1)

где р_i(х), f(x) определены и непрерывны в интервале (а,b).

Тогда уравнение (1) имеет единственное решение у = у(х), удовлетворяющее начальным условиям:

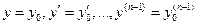при х = х₀, где а 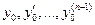- любые заданные числа. Это решение определено и n раз дифференцируемо для .

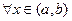Особых решений уравнение (1) не имеет. Если f(x)≡0, то уравнение (1) называется однородным:

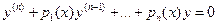, (2).

Для сокращения записи введём линейный дифференциальный оператор:

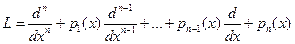, (3).

Тогда уравнение (1)можно записать в виде:

L[y] = f(x) (1), а однородное уравнение L[y] = 0 (2).

Запишем очевидные свойства оператора L:

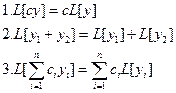
Определение. Функцию Z(x) = U(x) + iV(x) будем называть комплексной функцией от вещественной переменной х. U(x) u V(x) называются соответственно действительной и мнимой частями комплексной функции Z(x).

Теорема. Если комплексная функция у(х) является решением однородного уравнения (2), то её вещественная и мнимая части являются вещественными решениями этого уравнения.

Доказательство. y(x)=y₁(x)+i y₂(x) является решением уравнения (2).

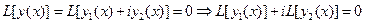. Тогда .

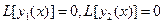Пример.