Аналитических методов оптимизации

Характеристика и классификация

 

Современное состояние теории электромеханических преобразо­вателей энергии характеризуется наличием развитой системы мате­матических моделей и алгоритмов анализа различных физических про­цессов в ЭМУС. Это открывает возможности для построения подхода к задачам поиска и оптимизации проектных решений на математической основе, с сокращением до минимума дорогостоящих и длительных процеду­р физического моделирования.

Различают аналитические и поисковые методы оптимизации.

Аналитическиеили классические ме­тоды оптимизации связаны с использованием возможностей и применением средств дифференциального и вариационного исчислений для определения экстремума функции це­ди. Эти методы позволяют определить точки, удовлетворяющие лишь необходимым признакам локальных экстремумов, для чего используются частные производные функции цели по параметрам. Поэтому применение классических методов возможно, только:

1) Если известно аналитическое выражение функции цели от параметров;

2) если эта функция дважды дифференцируема по параметрам.

Как известно, в точке экстремума все частные производные функции обращаются в нуль, т. е.

 

, i=1, 2, . . . , n. (2.1)

 

В соответствии с этим для определения местоположения экстремума используют необходимые и достаточные условия экстремума. Эти условия легко получить с помощью разложения в ряд Тейлора в окрестности точек :

 

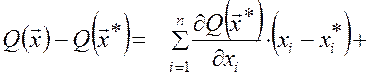
. (2.2)

 

 

Необходимое условие экстремума:

 

. (2.3)

 

Точки в пространстве параметров, для которых выполняется это условие, называются стационарными.

Достаточным условием максимума является отрицательность суммы членов со вторыми частными производными в окрестности точек , то есть:

 

, (2.4)

 

где – вектор-столбец; – вектор-строка;

 

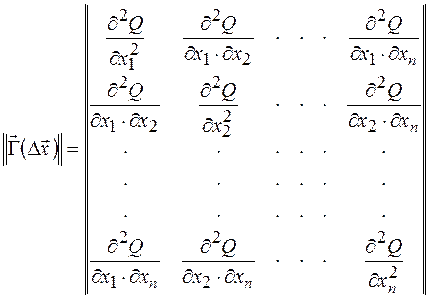
(2.5)

 

– матрица Гессе или гессиан.

Матрицу , удовлетворяющую условию (2.4) при любых , называют отрицательно определённой, а если выполняется условие

 

, (2.6)

 

то – положительно определённой.

Поэтому достаточные условия экстремума можно представить как требование отрицательной определённости матрицы Гессе для точки максимума или положительной определённости – для минимума в экстремальной точке.

Ограниченное применение аналитических методов для решения задач оптималь­ного проектирования или для оптимизации технических объектов и систем и, в частности, ЭМУС, обусловлено следующими причинами:

1) Всё сказанное относится к определению точки безусловного экстремума . А это условие, как правило, и не выполняется при оптимизации технических объектов, в частности ЭМУС

2) Отмеченные ранее неявновыраженность и частичная дискретность , наличие ограничений в виде равенств и неравенств вынуждают применять различные методы исследования внутренних и граничных точек в области допустимых значений .

3) Условия (2.1) справедливы не только для точек экстремума, но и для точек перегиба. Вся совокупность точек простран­ства параметров, удовлетворяющих условиям (2.1), как отмечено ранее, носит название стационарных точек. Поэтому при решении задач оптимизации необходимо определить все стационарные точки, а затем уже выделить из них точку глобального экстремума функции цели. Учитывая неявновыраженность функции цели относительно параметров оптимизации, характерную для математического описания ЭМУС, необходимо говорить, как правило, лишь о численных методах решения уравнений (2.1).

4) Ещё более проблематичным представляется применение аналити­ческих методов при отыскании условных экстремумов функ­ции цели, что характерно для решения задач оптимизации при нали­чии ограничений, т. е. в реальных задачах проектирования ЭМУС. Ог­раничения, накладываемые на область определения функции цели, при­водят к возможному несовпадению условных и локальных экстремумов, а поэтому уравнения (2.1) в данном случае нельзя рассматривать в качестве необходимых условий для определения точек экстремума.

5) Для определения экстремума Q в задачах с ограничениями рекомендуется отдельно рассматривать множества точек внутри и на границе области допустимых значений параметров S. Однако в настоящее время не существует общих методов исследования гранич­ных точек на экстремум. В частности, для ЭМУС, как правило, не имеется и явных выражений для ограничений, поэтому затруднитель­но даже само определение множества граничных точек.