Полный факторный эксперимент.
Полным факторным экспериментом (ПФЭ) называется эксперимент, реализующий все возможные неповторяющиеся комбинации уровней п независимых управляемых факторов, каждый из которых варьируют на двух уровнях. Число этих комбинаций N=2n определяет тип ПФЭ. Для упрощения дальнейшее изложение построим на примере планирования типа N==23, т. е. на примере объекта с тремя (n=3) независимыми управляемыми факторами x1,х2,х3. При планировании эксперимента проводят преобразование размерных управляемых независимых факторов хi, в безразмерные, нормированные:
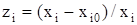 ; (3.15)
; (3.15)
это дает возможность легко построить ортогональную МП и значительно облегчает дальнейшие расчеты, так как в этом случае верхние и нижние уровни варьирования ziв и ziн в относительных единицах равны соответственно +1 и —1 независимо от физической природы факторов, значений основных уровней и интервалов варьирования факторов Dхi.
Если для трехфакторной задачи теоретическое уравнение регрессии относительно нормированных факторов имеет вид
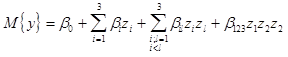 (3.16)
(3.16)
(т. е. степенями факторов выше первой можно пренебречь), то ПФЭ дает возможность найти раздельные оценки коэффициентов bi. Так как изменение выходной величины у носит случайный характер, то имеется возможность определить лишь выборочные коэффициенты регрессии bi,bil для оценивания теоретических коэффициентов bi,bil. Процесс нахождения модели (идентификации) методом ПФЭ состоит из: 1) планирования эксперимента; 2) проведения эксперимента на объекте исследования; 3) проверки воспроизводимости (однородности выборочных дисперсий  эксперимента; 4) получения математической модели объекта с проверкой статистической значимости выборочных коэффициентов регрессии; 5) проверки адекватности математического описания.
эксперимента; 4) получения математической модели объекта с проверкой статистической значимости выборочных коэффициентов регрессии; 5) проверки адекватности математического описания.
1.1 Планирование эксперимента. Матрицу планирования ПФЭ можно представить в виде табл. 3.2. Ее составляют по следующим правилам:
Таблица3.2
| G | zo | z1 | z2 | z3 | z1z2 | z1z3 | z2z3 | z1z2z3 |
| +1 +1 +1 +1 +1 +1 +1 +1 | -1 +1 -1 +1 -1 +1 -1 +1 | -1 -1 +1 +1 -1 -1 +1 +1 | -1 -1 -1 -1 +1 +1 +1 +1 | +1 -1 -1 +1 +1 -1 -1 +1 | +1 -1 +1 -1 -1 +1 -1 +1 | +1 +1 -1 -1 -1 -1 +1 +1 | -1 +1 +1 -1 +1 -1 -1 +1 |
1. Каждая g-я строка матрицы содержит набор координат zigточки, в которой проводится g-й опыт (i= 1,2,..., п; g= 1,2,..., N).
2. Как указывалось выше, вводят фиктивную переменную zo=+1.
3. Поскольку переменные zi принимают лишь значения +1 и -1, все взаимодействия zizl (i; l= 1, 2, 3; i¹l) могут принимать только такие же значения.
4. В первой строке (g= 1) все управляемые факторы выбирают на нижнем уровне, т. е. zi= -1. Последующие g-e варианты варьирования при составлении МП выбирают так: при построчном переборе всех вариантов частота смены знака факторов для каждого последующего фактора zi+1 вдвое меньше, чем для предыдущего zi (см. табл. 3.2). Три столбца управляемых факторов образуют собственно план эксперимента (обведено жирной чертой), а остальные столбцы МП получаются перемножением соответствующих значений управляемых факторов и необходимы для расчета соответствующих коэффициентов при взаимодействиях.
План ПФЭ типа 24 (n = 4) можно построить либо указанным выше способом, либо на базе плана ПФЭ типа 23, повторив его дважды: один раз — при величине z4= -1, второй раз — при z4=+1 Аналогично могут быть получены планы для сколь угодно большого числа п независимых управляемых факторов.
Необходимо отметить, что в тех случаях, когда влияние на отклик переменных типа Остановится существенным и появляется необходимость вычисления оценок коэффициентов при них, ПФЭ не дает возможности определить раздельные оценки таких коэффициентов, как bo,bii (i=l, 2, ..., п), поскольку соответствующие вектор-столбцы МП равны между собой, а потому эта матрица имеет линейно зависимые вектор-столбцы.
1.2 Проведение эксперимента на объекте исследования.Так как изменение отклика у носит случайный характер, то в каждой точке 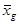 приходится проводить т параллельных опытов и результаты наблюдений yg1, yg2,..., ygm осреднять:
приходится проводить т параллельных опытов и результаты наблюдений yg1, yg2,..., ygm осреднять:
 . (3.17)
. (3.17)
 Пусть в рассматриваемом случае m=3. Перед реализацией плана на объекте необходимо рандомизировать варианты варьирования факторов, т.е. с помощью таблицы равномерно распределенных случайных чисел (литерат) или компьютерной программы для реализации процесса рандомизации определить последовательность реализации вариантов варьирования плана в Nm опытах. Пример рандомизации (g=8, m=3), приведен в таблице 3.1. Пусть, например, k1=8 при g=3; это значит, что третий вариант варьирования реализуется в эксперименте восьмым по порядку. Результаты наблюдений эксперимента соответственно вариантам варьирования плана записывают в столбцы
Пусть в рассматриваемом случае m=3. Перед реализацией плана на объекте необходимо рандомизировать варианты варьирования факторов, т.е. с помощью таблицы равномерно распределенных случайных чисел (литерат) или компьютерной программы для реализации процесса рандомизации определить последовательность реализации вариантов варьирования плана в Nm опытах. Пример рандомизации (g=8, m=3), приведен в таблице 3.1. Пусть, например, k1=8 при g=3; это значит, что третий вариант варьирования реализуется в эксперименте восьмым по порядку. Результаты наблюдений эксперимента соответственно вариантам варьирования плана записывают в столбцы  .
.
1.3 Проверка воспроизводимости эксперимента есть не что иное, как проверка выполнения второй предпосылки регрессионного анализа об однородности выборочных дисперсий 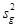 . Задача состоит в проверке гипотезы о равенстве генеральных дисперсий
. Задача состоит в проверке гипотезы о равенстве генеральных дисперсий 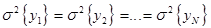 при опытах соответственно в точках
при опытах соответственно в точках 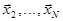 . Оценки дисперсий находят по известной формуле:
. Оценки дисперсий находят по известной формуле:
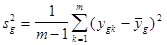 . (3.18)
. (3.18)
Так как все оценки дисперсий получены по выборкам одинакового объема т =3, то число степеней свободы для всех них одинаково и составляет
n1вос=m-1 (3.19)
В этом случае для проверки гипотезы об однородности оценок 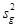 дисперсий следует пользоваться критерием Koxpэнa, который основан на законе распределения отношения максимальной оценки дисперсии к сумме всех сравниваемых оценок дисперсий, т.е.;
дисперсий следует пользоваться критерием Koxpэнa, который основан на законе распределения отношения максимальной оценки дисперсии к сумме всех сравниваемых оценок дисперсий, т.е.;
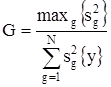 . (3.20)
. (3.20)
Если вычисленное по данным эксперимента (эмпирическое) значение критерия G окажется меньше критического значения Gкр, найденного по таблице (литерат) для n1вос=m-1 и n2вос=N (в данном случае n1вос =2 и n2вос=8) и выбранного уровня значимости qвос [%] (обычно 5 %), то гипотеза об однородности выборочных дисперсий отвечает результатам наблюдений. При этом всю группу выборочных дисперсий 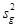 можно считать оценками для одной и той же генеральной дисперсии s2{у} воспроизводимости эксперимента, откуда наилучшая ее оценка имеет вид
можно считать оценками для одной и той же генеральной дисперсии s2{у} воспроизводимости эксперимента, откуда наилучшая ее оценка имеет вид
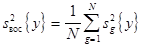 (3.21)
(3.21)
с числом степеней свободы
nзи=N(m-1) (3.22)
Если проверка воспроизводимости эксперимента дала отрицательный результат, то остается признать его невоспроизводимость относительно управляемых факторов вследствие наличия неблагоприятных флуктуаций неуправляемых и неконтролируемых факторов. При этом следует либо увеличить число параллельных опытов для вариантов варьирования с большими значениями выборочных дисперсий 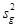 , либо использовать в дальнейшем модификацию метода наименьших квадратов, пригодную при невыполнении предпосылки о воспроизводимости эксперимента.
, либо использовать в дальнейшем модификацию метода наименьших квадратов, пригодную при невыполнении предпосылки о воспроизводимости эксперимента.
1.4 Получение математический модели объекта. При ПФЭ получаются независимые оценки bo, bi, bil соответствующих коэффициентов bo, bi, bil, т. е. bo®bo, bi®bi, bil®bil. Эти оценки легко найти по формулам
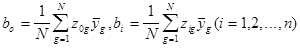 , (3.23)
, (3.23)
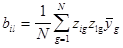 (i;l=1,2,...,n;i¹l).
(i;l=1,2,...,n;i¹l).
После определения оценок b коэффициентов регрессии необходимо проверить гипотезы об их значимости, т. е. проверить соответствующие нуль-гипотезы b=0. Проверку таких гипотез производят с помощью критерия Стьюдента, эмпирическое значение которого
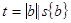 , (3.24)
, (3.24)
где
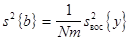 (3.25)
(3.25)
—дисперсия оценки b коэффициента; N— число точек факторного пространства, в которых проводится эксперимент; т— число параллельных опытов в этих точках. Если найденная величина параметра t превышает значение tкр, определенное из Приложения V для числа степеней свободы nзи=N(m-1), при заданном уровне значимости qзи (обычно 5'%), т. е. sign (t-tкр) = +1, то проверяемую нуль-гипотезу Но:b=0 отвергают и соответствующую оценку b коэффициента признают значимой.
В противном случае, т. е. при sign(t-tкр)= -1, нуль-гипотезу не отвергают и оценку b считают статистически незначимой, т. е. b=0.
Статистическая незначимость оценки bi коэффициента регрессии может быть обусловлена следующими причинами:
1) данный i-й фактор не имеет функциональной связи с откликом у, т. е. bi=0;
2) уровень хio базового режима 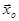 находится в точке частного экстремума функции отклика по фактору хi и тогда
находится в точке частного экстремума функции отклика по фактору хi и тогда 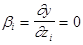 ;
;
3) интервал варьирования Dxi выбран малым;
4) вследствие влияния неуправляемых и неконтролируемых факторов велика ошибка воспроизводимости эксперимента.
Ортогональное планирование позволяет определять доверительные границы независимо для каждого из коэффициентов регрессии. Потому если какая-либо из оценок коэффициентов окажется незначимой, то ее можно отбросить без пересчета всех остальных. После этого математическую модель объекта составляют в виде, уравнения связи отклика у и факторов г„ включающего только значимые оценки коэффициентов.
1.5 Проверка адекватности математического описания. Чтобы проверить гипотезу об адекватности математического описания опытным данным, достаточно оценить отклонение предсказанной по полученному уравнению регрессии величины отклика  от результатов наблюдений
от результатов наблюдений 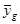 в одних и тех же g-х точках факторного пространства. Рассеяние результатов наблюдений вблизи уравнения регрессии, оценивающего истинную функцию отклика, можно охарактеризовать с помощью дисперсии адекватности
в одних и тех же g-х точках факторного пространства. Рассеяние результатов наблюдений вблизи уравнения регрессии, оценивающего истинную функцию отклика, можно охарактеризовать с помощью дисперсии адекватности
 , (3.26)
, (3.26)
где d — число членов аппроксимирующего полинома. Дисперсия адекватности определяется с числом степеней свободы
nад=N-d. (3.27)
Проверка гипотезы об адекватности состоит, по сути дела. в выяснении соотношения между дисперсией адекватности 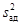 и оценкой дисперсии воспроизводимости отклика
и оценкой дисперсии воспроизводимости отклика  . Если эти оценки дисперсий однородны, то математическое описание адекватно представляет результаты опыта; если же нет, то описание считается неадекватным. Проверку гипотезы об адекватности производят с использованием F-критерия Фишера. Критерий Фишера позволяет проверить гипотезу об однородности двух выборочных дисперсий
. Если эти оценки дисперсий однородны, то математическое описание адекватно представляет результаты опыта; если же нет, то описание считается неадекватным. Проверку гипотезы об адекватности производят с использованием F-критерия Фишера. Критерий Фишера позволяет проверить гипотезу об однородности двух выборочных дисперсий 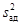 и
и  {у}- В том случае, если
{у}- В том случае, если 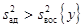 , F-критерий характеризуется отношением
, F-критерий характеризуется отношением
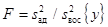 (3.28)
(3.28)
Если вычисленное по результатам наблюдений эмпирическое значение критерия F меньше критического Fкр, найденного из (литерат) для соответствующих степеней свободы
n1ад=N-d, n2ад=nзн=N(m-1) (3.29)
при заданном уровне значимости qад, то гипотезу об адекватности не отвергают. В противном случае гипотезу отвергают и математическое описание признается неадекватным.
Проверка адекватности возможна при n1ад> 0. Если число N вариантов варьирования плана ПФЭ равно числу всех значимых оценок коэффициентов регрессии (N =d), то для проверки гипотезы об адекватности математического описания степеней свободы не остается (n1ад= 0). Если же некоторые оценки коэффициентов регрессии оказались незначимыми, то число d членов проверяемого уравнения в этом случае меньше числа N вариантов варьирования {N>d) и для проверки гипотезы об адекватности останется одна или несколько степеней свободы (n1ад>0).
В том случае, когда гипотеза об адекватности отвергается, необходимо переходить к более сложной форме математического описания либо, если это возможно, проводить эксперимент с меньшим интервалом варьирования Dхi. Следует отметить, что максимальная величина интервала варьирования определяется условием адекватного описания объекта в области варьирования. Если при больших интервалах варьирования математическая модель неадекватна, то возникают систематические ошибки в определении коэффициентов, для уменьшения которых следует сузить область варьирования. Однако с уменьшением интервала варьирования появляется целый ряд новых трудностей: растет отношение помехи к полезному сигналу, что приводит к необходимости увеличивать число параллельных опытов для выделения полезного сигнала на фоне шума, т. е. уменьшаются абсолютные значения оценок bi, коэффициентов, величины которых непосредственно зависят от Dxi;(для уравнения c нормированными факторами zi), и оценки коэффициентов могут стать статистически незначимыми.
Для выбора интервала варьирования проводят предварительные эксперименты. Интервал варьирования можно выбирать равным 0,05—0,3 от допустимого диапазона варьирования факторов, т.е. область варьирования составляет примерно 10—60% от всего диапазона. Начальную точку варьирования (базовую точку) выбирают возможно ближе к центру области факторного пространства, в которой ищется математическое описание объекта (или области ограничений).