Зависимость погрешностей от значения измеряемой величины.
В зависимости от вида функции преобразования прибора (преобразователя) его общая погрешность и ее составляющие различным образом зависят от значения измеряемой величины. Рассмотрим эти зависимости при разных функциях преобразования 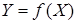 .
.
I. Зависимость Δ(X) и σ(X) при линейной функции Y = SX (Аддитивная и мультипликативная погрешности. Порог чувствительности)
Как уже отмечалось, функция преобразования вида 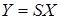 присуща большинству измерительных приборов. При этом результирующая погрешность на выходе прибора
присуща большинству измерительных приборов. При этом результирующая погрешность на выходе прибора  (в единицах выходной величины
(в единицах выходной величины 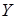 ) может возникать:
) может возникать:
– во-первых, за счет аддитивного наложения на входную измеряемую величину 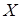 некоторой малой неконтролируемой величины
некоторой малой неконтролируемой величины 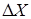 (например, шумы или наводки);
(например, шумы или наводки);
– во-вторых, из-за наличия аналогичной 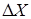 величины
величины 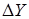 на выходе прибора — например, в случае дискретного характера (квантования) выходного сигнала
на выходе прибора — например, в случае дискретного характера (квантования) выходного сигнала 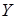 (входной сигнал
(входной сигнал 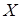 обычно имеет неправильный (аналоговый) характер);
обычно имеет неправильный (аналоговый) характер);
– в третьих, за счет малых неконтролируемых изменений (нестабильности) 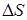 чувствительности
чувствительности 
Причем 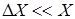 ,
, 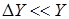 ,
, 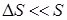 . С учетом этих факторов значение
. С учетом этих факторов значение  на выходе, очевидно, будет отличаться от теоретического значения
на выходе, очевидно, будет отличаться от теоретического значения 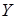 на величину
на величину  :
:
 (1)
(1)
(В (1) слагаемым  , имеющим более высокий порядок малости, пренебрегли). Из (1) следует, что результат измерения
, имеющим более высокий порядок малости, пренебрегли). Из (1) следует, что результат измерения 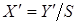 величины
величины 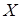 может быть представлен в виде
может быть представлен в виде
 (2)
(2)
Здесь  — абсолютная погрешность измерения, выраженная, как и полагается, в единицах
— абсолютная погрешность измерения, выраженная, как и полагается, в единицах 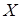 , и состоящая из двух слагаемых: первое из них
, и состоящая из двух слагаемых: первое из них  называется аддитивной погрешностью(от add – прибавлять) поскольку она, как видим, суммируется с
называется аддитивной погрешностью(от add – прибавлять) поскольку она, как видим, суммируется с 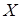 и не зависит от него. Второе слагаемое
и не зависит от него. Второе слагаемое 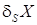 называется мультипликативной погрешностью (от multiply – умножать), так как оно определяется умножением измеряемого значения на относительную погрешность чувствительности
называется мультипликативной погрешностью (от multiply – умножать), так как оно определяется умножением измеряемого значения на относительную погрешность чувствительности
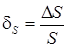 (3)
(3)
Таким образом, в случае линейной функции преобразования абсолютная погрешность измерения
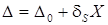 (4)
(4)
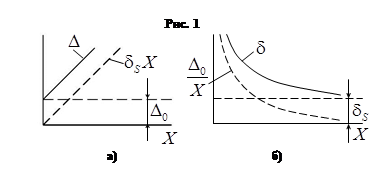 |
в общем случае состоит из суммы аддитивной и мультипликативной погрешностей. Первая из них не зависит от измеряемой величины, а вторая — пропорциональна ей (рис 1а). При этом важно отметить, что так ведут себя в зависимости от
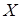 абсолютные (размерные) значения этих погрешностей.
абсолютные (размерные) значения этих погрешностей.
Поскольку с увеличением 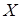 возрастает общая погрешность
возрастает общая погрешность 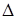 , может показаться, что с ростом измеряемой величины точность измерения будет уменьшаться. Однако, согласно (4) относительная погрешность
, может показаться, что с ростом измеряемой величины точность измерения будет уменьшаться. Однако, согласно (4) относительная погрешность 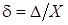 , характеризующая, как известно, точность измерения, равна
, характеризующая, как известно, точность измерения, равна
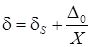 , (5)
, (5)
Из (5) следует два важных вывода. Во-первых, при представлении погрешности 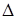 в относительном (безразмерном) виде
в относительном (безразмерном) виде 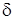 , ее мультипликативная составляющая становится равной погрешности чувствительности
, ее мультипликативная составляющая становится равной погрешности чувствительности 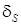 , которая не зависит от значения измеряемой величины
, которая не зависит от значения измеряемой величины 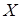 , а аддитивная составляющая оказывается обратно пропорциональной
, а аддитивная составляющая оказывается обратно пропорциональной 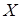 (рис. 1б).
(рис. 1б).
Во-вторых, при линейной функции преобразования точность измерения повышается с увеличением измеряемой величины. Отсюда практическая рекомендация: при линейной функции преобразования в целях повышения точности измерения следует выбирать диапазон измерений так, чтобы предполагаемое значение измеряемой величины находилось как можно ближе к верхнему приделу шкалы прибора. Из (4), (5) и рис. 1 видно, что при больших значениях измеряемой возрастает вклад мультипликативной составляющей в общую погрешность, и, наоборот, при малых 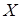 основную часть погрешности составляет аддитивная погрешность.
основную часть погрешности составляет аддитивная погрешность.
На практике погрешности измерения конкретным прибором обычно бывают заданы лишь в виде некоторых допустимых (предельных) значений  или
или 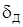 со знаком
со знаком  .
.
Например, в техническом описании серийно выпускаемого цифрового частотомера (с линейной функцией преобразования) может быть указано, что основная погрешность измерения частоты 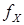 не превышает значения, которое может быть задано либо в абсолютных значениях:
не превышает значения, которое может быть задано либо в абсолютных значениях:
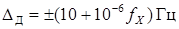 , (6)
, (6)
где первое слагаемое — аддитивная, а вторая — мультипликативная погрешность, либо в относительных значениях:
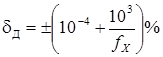 , (7)
, (7)
где вначале указана погрешность чувствительности (мультипликативная), а за ней относительная аддитивная составляющая. Разумеется, в конечном экземпляре такого частотомера или при конкретном измерении погрешность может быть меньше указанного предела.
 С учетом такой неопределенности задания погрешности выходную величину
С учетом такой неопределенности задания погрешности выходную величину 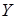 следует считать связанной с входной величиной
следует считать связанной с входной величиной 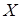 соотношением
соотношением 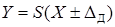 , где
, где  увеличивается с ростом
увеличивается с ростом 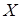 из-за мультипликативной составляющей. При этом вместо номинальной зависимости
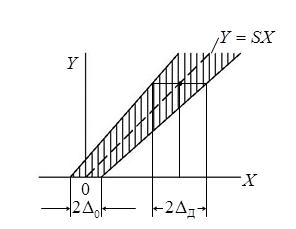
из-за мультипликативной составляющей. При этом вместо номинальной зависимости 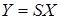 в виде прямой линии получается расширяющаяся полоса шириной
в виде прямой линии получается расширяющаяся полоса шириной 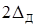 (рис. 2), характеризующая зону неопределенности измерений, т. е. неопределенности наших знаний о действительном значении
(рис. 2), характеризующая зону неопределенности измерений, т. е. неопределенности наших знаний о действительном значении 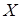 .
.
Поскольку минимальная ширина этой полосы равна 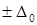 , ясно, что значение измеряемой величины
, ясно, что значение измеряемой величины 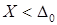 прибор не сможет достоверно отличить от нуля. Таким образом, минимально различимым значением, на которое достоверно реагирует прибор, является
прибор не сможет достоверно отличить от нуля. Таким образом, минимально различимым значением, на которое достоверно реагирует прибор, является 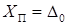 . Это значение, определяемое аддитивной погрешностью, называется порог чувствительности данного прибора.
. Это значение, определяемое аддитивной погрешностью, называется порог чувствительности данного прибора.
II. Зависимость погрешности от измеряемой величины при нелинейной функции преобразования вида Y = a / (b + X)
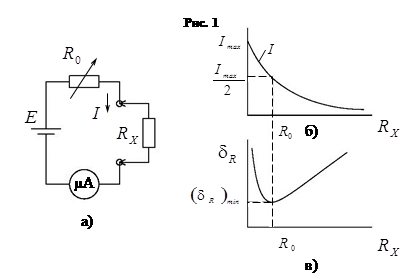
Нетрудно выяснить, что преобразование такого вида выполняется в простейшем омметре со стрелочным указателем — микроамперметром (рис 3а). Измеряемой величиной является 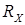 , а выходной — ток
, а выходной — ток 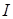 :
:
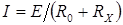 (8)
(8)
Из (8) видно, что, во-первых, шкала такого прибора нелинейна, т. е. неравномерна. Во-вторых, входная и выходная величины находятся в обратной зависимости — большему значению 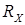 соответствует меньший ток
соответствует меньший ток 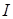 (рис 3б). Начало шкалы прибора, соответствующее
(рис 3б). Начало шкалы прибора, соответствующее  должно соответствовать максимальному току указателя
должно соответствовать максимальному току указателя 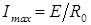 , а конец шкалы при
, а конец шкалы при 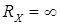 должен соответствовать нулю тока. Обычно перед измерением проверяют правильность градуировки шкалы: при разомкнутом входе (
должен соответствовать нулю тока. Обычно перед измерением проверяют правильность градуировки шкалы: при разомкнутом входе (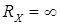 ) убеждаются, что стрелка находится на крайнем левом делении, а при короткозамкнутом входе (
) убеждаются, что стрелка находится на крайнем левом делении, а при короткозамкнутом входе ( и
и 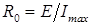 ) — на крайнем правом. При необходимости последнее условие выполняют изменяя
) — на крайнем правом. При необходимости последнее условие выполняют изменяя 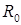 .
.
Считая, что погрешность 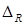 измерения
измерения 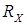 определяется погрешностью измерения тока
определяется погрешностью измерения тока 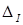 , продифференцируем
, продифференцируем 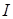 по
по 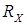 :
:
 (9)
(9)
Отсюда
 (10)
(10)
Знак минус в (10) отражает обратную зависимость 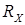 и
и 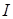 . Но поскольку погрешность обычно указывается с двойным знаком
. Но поскольку погрешность обычно указывается с двойным знаком  , этот минус в дальнейшем не будем учитывать.
, этот минус в дальнейшем не будем учитывать.
Выразим относительную погрешность измерения:
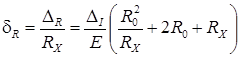 (11)
(11)
Из (11) видно, что  при
при 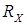 стремящемся к 0 и к
стремящемся к 0 и к  . Это значит, что есть
. Это значит, что есть 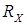 , при котором
, при котором  будет минимальна. Известно, что для нахождения координат минимума зависимости
будет минимальна. Известно, что для нахождения координат минимума зависимости  необходимо приравнять нулю производную
необходимо приравнять нулю производную  по
по 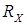 :
:

Откуда следует, что  при
при  (рис 3в). Подставив это значение
(рис 3в). Подставив это значение 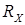 в (11), найдем
в (11), найдем
 (12)
(12)
где 
 есть приведенная погрешность микроамперметра, характеризующая его класс точности.
есть приведенная погрешность микроамперметра, характеризующая его класс точности.
Сам по себе стрелочный указатель имеет линейную функцию преобразования  (
( — угол отклонения стрелки) и, следовательно, равномерную шкалу по току
— угол отклонения стрелки) и, следовательно, равномерную шкалу по току 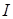 . Отсюда следует, что если
. Отсюда следует, что если  , а значит
, а значит  минимальна и
минимальна и  , то стрелка будет находиться посредине шкалы (рис 3б).
, то стрелка будет находиться посредине шкалы (рис 3б).
Итак, во-первых, при рассмотренном виде нелинейного преобразования минимум относительной погрешности находится в середине шкалы. Значит надо соответствующим образом выбирать диапазон шкалы 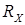 . Во-вторых, из (12) следует, что этот минимум в 4 раза больше приведенной (минимальной) погрешности указателя (см (12)).
. Во-вторых, из (12) следует, что этот минимум в 4 раза больше приведенной (минимальной) погрешности указателя (см (12)).