Уравнение непрерывности

На рис. 2.2. показана замкнутая поверхность внутри проводника, в котором течет ток. Поверхность ограничивает объем , - единичная внешняя нормаль к элементу поверхности .

Рис. 2.2. К выводу уравнения непрерывности

 

В соответствии с законом сохранения заряда сила тока 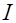через поверхность равна скорости убыли заряда в объеме :

 

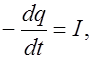(2.4)

 

где сила тока 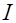выражается формулой (2.3), а

 

(2.5)

 

Уравнение (2.4) выражает закон сохранения заряда в интегральном виде.

Пусть поверхность неподвижна. Тогда скорость движения объема равна нулю: , и в (2.4) полную производную по времени 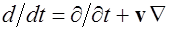можно заменить на частную . Подставим (2.3) и (2.5) в (2.4), найдем

(2.6)

 

Правую часть уравнения (2.6) выразим с помощью формулы Гаусса-Остроградского

(2.7)

 

Перепишем (2.6) с учетом (2.7) как

 

(2.8)

 

Равенство (2.8) должно выполняться тождественно независимо от выбора объема . Тогда из (2.8) и (2.1) следует уравнение непрерывности электрического тока

(2.9)

 

которое выражает закон сохранения электрического заряда в дифференциальном виде.

Применим закон сохранения заряда (2.4) для постоянного тока, когда заряд в объеме не изменяется, то есть . Получим , то есть

(2.10)

 

Пучок выделенных линий тока образует трубку тока (см. рис. 2.3).

 

 

Рис. 2.3. Трубка постоянного тока

 

Применительно к трубке постоянного тока из (2.10) получаем

 

(2.11)

 

Сила тока через боковую поверхность трубки равна нулю, так как линии тока эту поверхность не пересекают, то есть

 

 

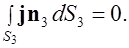
Сила тока, втекающего в выделенный объем трубки через поверхность равна

 

а вытекающего из этого объема через поверхность -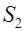

 

 

В результате из (2.11) следует

 

Вывод.Сила постоянного тока через любое сечение трубки тока одна и та же.

Заметим, что трубка тока может быть образована телом проводника, по которому течет ток.