Связь потенциала с напряженностью электростатического поля
Пусть  - вектор бесконечно малого смещения пробного заряда
- вектор бесконечно малого смещения пробного заряда 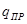 из точки с потенциалом
из точки с потенциалом  в точку с потенциалом
в точку с потенциалом  . Величина работы по перемещению заряда равна
. Величина работы по перемещению заряда равна
 ,
,
откуда
 (1.27)
(1.27)
Формула (1.27) показывает, что вектор напряженности электрического поля в каждой точке указывает направление, при смещении в котором потенциал поля падает наиболее быстро (так как  и
и  ). Величина напряженности поля
). Величина напряженности поля  характеризует скорость изменения потенциала в том же направлении в точке
характеризует скорость изменения потенциала в том же направлении в точке  . Перепишем (1.27):
. Перепишем (1.27):
 . (1.28)
. (1.28)
В декартовой системе координат  с ортами
с ортами  :
:
 (1.29)
(1.29)
Введем дифференциальный оператор  - «набла», который обладает всеми свойствами вектора и в декартовой системе координат
- «набла», который обладает всеми свойствами вектора и в декартовой системе координат  с ортами
с ортами  имеет вид:
имеет вид:
 (1.30)
(1.30)
Умножение вектора  на скаляр
на скаляр  - дифференциальная операция первого порядка, называемая взятием градиента скалярной функции
- дифференциальная операция первого порядка, называемая взятием градиента скалярной функции  . Из исходного поля скалярной функции
. Из исходного поля скалярной функции  получается производное векторное поле:
получается производное векторное поле:
 (1.31)
(1.31)
С учетом (1.31) перепишем (1.29):
 . (1.32)
. (1.32)
Сравнивая (1.28) с (1.32), получаем формулу связи потенциала с напряженностью электрического поля:
 (1.33)
(1.33)
Из (1.31) и (1.33) находим декартовы компоненты вектора  :
:  и модуль этого вектора:
и модуль этого вектора:
 (1.34)
(1.34)
Формула (1.27) показывает, что при смещении  из точки
из точки  поперек направления
поперек направления  потенциал сохраняет постоянное значение.
потенциал сохраняет постоянное значение.
Определение.Каждая поверхность, на которой потенциал сохраняет заданное постоянное значение, называется эквипотенциальной.
В каждой своей точке эквипотенциальная поверхность перпендикулярна вектору напряженности поля в той же точке. Так, эквипотенциали поля точечного заряда  в соответствии с (1.23) представляют собой концентрические сферы с центром в точке расположения заряда
в соответствии с (1.23) представляют собой концентрические сферы с центром в точке расположения заряда  .
.

 Рис. 1.12. Эквипотенциали электрического поля точечного заряда
Рис. 1.12. Эквипотенциали электрического поля точечного заряда