Потенциалов электрического поля
Работа в электрическом поле. Потенциал и разность
Пусть электрическое поле  создано неподвижным точечным зарядом
создано неподвижным точечным зарядом  . В любой точке поля на точечный заряд
. В любой точке поля на точечный заряд  со стороны поля действует сила (см. рис. 1.10)
со стороны поля действует сила (см. рис. 1.10)
 (1.15)
(1.15)
где  - величина силы
- величина силы  ,
,  - орт в направлении от заряда
- орт в направлении от заряда  к заряду
к заряду  .
.

Рис. 1.10. Движение заряда  в электростатическом поле заряда
в электростатическом поле заряда 
вдоль траектории из точки 1 в точку 2,
 - вектор бесконечно малого смещения заряда
- вектор бесконечно малого смещения заряда  вдоль траектории движения,
вдоль траектории движения,
 - проекция вектора смещения
- проекция вектора смещения  на направление силы
на направление силы  , действующей на заряд
, действующей на заряд  со стороны электрического поля заряда
со стороны электрического поля заряда 
Работа, совершаемая полем по переносу заряда  из точки 1 в точку 2 вдоль траектории движения заряда равна
из точки 1 в точку 2 вдоль траектории движения заряда равна
 (1.16)
(1.16)
и не зависит от формы пути перемещения, а лишь положения в поле точек начала и конца перемещения ( на рис. 1.11). Такое поле называется потенциальным.
на рис. 1.11). Такое поле называется потенциальным.
Если  , то работа совершается силами самого поля. . Если
, то работа совершается силами самого поля. . Если  , то работа совершается против сил поля.
, то работа совершается против сил поля.
Работа по переносу тела под действием силы  по замкнутому контуру
по замкнутому контуру  , например,
, например,  , выражается интегралом
, выражается интегралом
 (1.17)
(1.17)
который называется циркуляцией вектора силы вдоль замкнутого контура  ,
,  - элемент смещения вдоль контура.
- элемент смещения вдоль контура.

Рис. 1.11. К обоснованию потенциальности электростатического поля
В соответствии с (1.16) для электрического заряда в электростатическом поле имеем:  Поэтому работа по переносу заряда
Поэтому работа по переносу заряда  по замкнутому контуру в электростатическом поле
по замкнутому контуру в электростатическом поле  . Но
. Но  . Отсюда вместо (1.17) получаем
. Отсюда вместо (1.17) получаем
 (1.18)
(1.18)
то есть циркуляция вектора напряженности электростатического поля по замкнутому контуру равна нулю.
Любое электростатическое поле является потенциальным, так как его всегда можно представить наложением полей точечных зарядов той или иной системы.
В соответствии с законом сохранения энергии работа, совершаемая потенциальным полем по переносу тела равна убыли потенциальной энергии тела. В частности, для заряда  на рис. 1.10 получаем
на рис. 1.10 получаем
 (1.19)
(1.19)
где  и
и  - значения потенциальной энергии заряда в положении 1 и 2, соответственно.
- значения потенциальной энергии заряда в положении 1 и 2, соответственно.
Сравнивая (1.16) с (1.18), находим выражение потенциальной энергии заряда  в произвольной точке
в произвольной точке  поля заряда
поля заряда  :
:
 (1.20)
(1.20)
Потенциальная энергия определена с точностью до произвольной постоянной. Физический смысл имеет не сама потенциальная энергия, а разность ее значений, определяющая работу, совершаемую полем. Для выбора значения  в (1.20) воспользуемся одним из множества возможных условий нормировки поля:
в (1.20) воспользуемся одним из множества возможных условий нормировки поля:
 .
.
Тогда
 . (1.21)
. (1.21)
Согласно (1.23), потенциальная энергия заряда  пропорциональна величине этого заряда и также зависит от свойств самого поля. Величина же
пропорциональна величине этого заряда и также зависит от свойств самого поля. Величина же  характеризует само поле и не зависит от величины заряда
характеризует само поле и не зависит от величины заряда  .
.
Определение.Потенциалом  любого электростатического поля в точке
любого электростатического поля в точке  называется скалярная характеристика этого поля, численно равная потенциальной энергии в расчете на единицу величины пробного заряда в той же точке:
называется скалярная характеристика этого поля, численно равная потенциальной энергии в расчете на единицу величины пробного заряда в той же точке:
 (1.22)
(1.22)
С учетом (1.20) и (1.21) из (1.22) потенциал поля точечного заряда  равен
равен

 (1.23)
(1.23)
Пусть поле создано системой точечных неподвижных зарядов  . Потенциал поля заряда
. Потенциал поля заряда  равен
равен  , где
, где  - радиус-вектор, проведенный от заряда
- радиус-вектор, проведенный от заряда  в точку наблюдения. Обозначим
в точку наблюдения. Обозначим  - радиус-вектор точки наблюдения, проведенный из начала системы координат. Потенциальная энергия пробного заряда
- радиус-вектор точки наблюдения, проведенный из начала системы координат. Потенциальная энергия пробного заряда 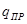 в поле заряда
в поле заряда  равна
равна  . Полная потенциальная энергия заряда
. Полная потенциальная энергия заряда 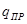 в поле системы зарядов равна
в поле системы зарядов равна  .Отсюда следует, что потенциал поля системы зарядов равен алгебраической сумме потенциалов полей отдельных зарядов системы:
.Отсюда следует, что потенциал поля системы зарядов равен алгебраической сумме потенциалов полей отдельных зарядов системы:

 (1.24)
(1.24)
В соответствии с (1.19) – (1.21) для перемещения пробного заряда 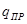 из данной точки поля с потенциалом
из данной точки поля с потенциалом  на бесконечность требуется совершить работу
на бесконечность требуется совершить работу
 (1.25)
(1.25)
В соответствии с (1.25) за единицу потенциала в системе СИ – 1 В, принимают потенциал в точки поля, для перемещения в которую единичного положительного заряда из бесконечности требуется совершить работу 1 Дж. Часто используется также единица измерения энергии 1 эВ. Электронвольт равен величине работы поля над элементарным зарядом при перемещении заряда между точками поля с падением потенциала 1 В ( ).
).
Выражения (1.20) и (1.21) позволяют выразить потенциальную энергию взаимодействия двух точечных зарядов -  и
и  , входящих в систему зарядов
, входящих в систему зарядов  :
:

где  - расстояние между этими зарядами.
- расстояние между этими зарядами.
Каждый заряд взаимодействует попарно со всеми остальными зарядами системы. Энергия обладает свойством аддитивности. Поэтому полная энергия взаимодействия зарядов системы равна
 (1.26)
(1.26)