Электростатическое поле и его напряженность

Взаимодействие неподвижных электрических зарядов осуществляется посредством электростатического поля, которое не зависит от времени. Поле заряда изменяет свойства окружающего пространства. Поле выделенного заряда проявляет себя, а значит, может быть обнаружено по силовому воздействию на другие заряды, помещенные в это поле.

Для обнаружения и исследования электрического поля в него вносят «пробный» заряд. Чтобы сила, действующая на «пробный» заряд со стороны поля, характеризовала поле в одной точке, «пробный» заряд должен быть точечным. «Пробный» заряд должен иметь достаточно малую величину, чтобы можно было пренебречь воздействием создаваемого им электрического поля на другие заряды в окружающем пространстве.

Пусть на пробный электрический заряд 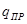, помещенный в некоторую точку электростатического поля , действует сила . Сила зависит не только от свойств самого поля в точке , но и от величины и знака пробного заряда .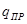

В частности, если поле создано неподвижным точечным зарядом , то в соответствии с рис. 1.6 и закона Кулона имеем:

 

(1.9)

 

где - орт радиус-вектора , , .

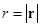Рис. 1.6. К формуле (1.9) для случая одноименных зарядов

 

Из (1.9) следует, что отношение силы, действующей на пробный заряд к величине этого заряда:

(1.10)

 

характеризует только поле заряда в точке и не зависит от величины и знака пробного заряда 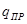, помещенного в точку .

Пусть поле создано системой неподвижных точечных зарядов (см. рис. 1.7).

 

Рис. 1.7. К формуле (1.11)

 

Согласно принципу суперпозиции (1.8), на пробный заряд 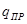со стороны зарядов системы действует сила

 

(1.11)

 

Из (1.11) следует, что отношение силы, действующей на пробный заряд к величине этого заряда:

(1.12)

 

характеризует только поле системы зарядов в точке и не зависит от величины и знака пробного заряда 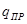, помещенного в точку .

Определение.Напряженность электрического поля - это его силовая векторная характеристика, значение которой в каждой заданной точке численно равно силе, действующей со стороны поля на единичный пробный заряд, помещенный в указанную точку.

Простейшее поле - однородное, вектор напряженности которого - постоянный. Формула (1.10) выражает напряженность электрического поля точечного заряда, а формула (1.12) – напряженность электрического поля системы точечных зарядов. Из (1.10) и (1.12) следует

(1.13)

 

где - напряженность электрического поля системы точечных зарядов, - напряженность электрического поля заряда в той же точке наблюдения .

Формула (1.13) выражает принцип суперпозиции (наложения) электрических полей: напряженность поля системы зарядов равна векторной сумме напряженностей полей, которые создавал бы каждый из зарядов системы в отдельности.

Принцип суперпозиции позволяет свести расчет напряженности поля системы зарядов к расчету напряженностей полей точечных зарядов, входящих в систему.

Из (1.12) следует, что сила, действующая на точечный заряд, пропорциональна как величине этого заряда, так и напряженности поля в точке, где находится этот заряд:

(1.14)

 

Единица измерения напряженности электрического поля в системе СИ: .

Геометрической характеристикой электрического поля служат его силовые линии (линии напряженности, см. рис. 1.8).

Рис. 1.8. Силовые линии электрического поля

 

Определение.Силовой линией электрического поля называется линия, касательная в каждой своей точке вектору напряженности поля в той же точке.

В окрестности каждой точки поля густота проведения силовых линий выбирается пропорциональной модулю вектора напряженности поля. Значит, по картине силовых линий поля можно судить не только о направлении вектора поля , но и модуле этого вектора. Через каждую точку, где , можно провести только одну силовую линию. В каждой точке, где , направление вектора поля не определено. Силовые линии электростатического поля могут начинаться на положительных зарядах, а заканчиваться на отрицательных зарядах или уходить на бесконечность. На рис. 1.9 приведены картины силовых линий поля положительного (а) и отрицательного (б) точечных зарядов.

Рис. 1.9. Картины силовых линий электрического поля положительного

и отрицательного точечного заряда