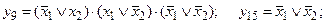Элементы булевой алгебры

Как уже говорилось при рассмотрении истории компьютерной техники, основу работы схем и устройств компьютера составляет специальный математический аппарат, называемый булевой алгеброй, алгеброй логики или исчислением высказываний. При этом под высказыванием понимается любое утверждение, о котором можно сказать, что оно истинно или ложно.

Если высказывание истинно, то считают, что его значение равно единице; если высказывание ложно, то считают, что его значениеравно нулю. Таким образом, значения высказываний можно рассматривать как переменную величину, принимающую только два дискретных значения: 0 или 1. Это приводит к полному соответствию между логическими высказываниями в математической логике и двоичными цифрами в двоичной системе счисления, что позволяет описывать работу логических схем компьютера, проводить их анализ и синтез с помощью математического аппарата алгебры логики.

Всякое устройство компьютера, выполняющее арифметические или логические операции, можно рассматривать как функциональный преобразователь, входными переменными (аргументами) которого являются исходные двоичные числа xi (i=1,n), а выходными функциями – yj (j=1,m) (рис. 1.2.10).

 

 

Рис. 1.2.10. Функциональный преобразователь – устройство компьютера

 

В этом случае функциями

yj = f(x1,x2,…xn),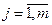

где:

xi – i-й вход;

n – число входов;

yj – j-й выход;

m – число выходов,

можно описывать алгоритм работы любого устройства компьютера.

Входные переменные, так и выходные функции могут принимать лишь одно из двух возможных значений: 0 или 1, иначе говоря, аргументы и функции определены на множестве из двух чисел: 0 и 1 (это записывается как xi,yiÎ{0,1}).

Алгебра логики устанав­ливает основные законы формирования и преобразования логических функций. Она позволяет представить любую сложную функцию в виде композиции простейших функций. Рассмотрим наиболее употребительные логические функции.

Так как каждая переменная xi при этом равна 0 или 1, то для n переменных образуется множество разнообразных сочетаний или наборов входных переменных. Количество функций N от n аргументов выражается следующей зависимостью:

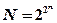. (1.2.1)

Для n=0 определены две основные функции, не зависящие от каких-либо переменных: y0, тождественно равную нулю (y0º0), и y1, тождественно равную единице (y1º1). Технической интер­претацией функции y1º1 может быть генератор импульсов. При от­сутствии входных сигналов на выходе этого устройства всегда име­ются импульсы (единицы). Функция y0º0 может быть интерпретиро­вана отключенной схемой, сигналы от которой не поступают ни к каким устройствам.

При n=1 зависимость (1.2.1) дает N=4. Представим зависимость зна­чений этих функций от значения аргумента x в виде специальной таб­лицы истинности (табл. 1.2.2), определяющей значение функции в зависимости от комбинации вход­ных сигналов.

 

Табл. 1.2.3. Таблица истинности для одного аргумента

x1 yj
y0 y1 y2 y3

Функции y0 и y3 имеют тот же смысл, что и функции y0 и y1 для n=0. Функция y1=x повторяет значение x, а функция y2 выдает значение, обратное значению x, и называется инверсией, или отрицанием x (отрицание обозначается 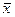, т. е. 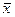= 0, если х = 1 , и 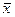= 1, еслиx = 0). Этим функциям соответствуют определенные технические анало­ги. Схема, реализующая зависимость у=х, называетсяповторите­лем, а схема y=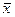–инвертором.

При n=2, значение N равно 16, т.е. от двух переменных можно построить шестнадцать различных логических функций y1, y2,..., y16. Эти функции приведены в табл. 1.2.4.

Табл. 1.2.4. Таблица истинности для двух аргументов

xi yj
x1 x2 y1 y2 y3 y4 y5 y6 y7 y8 y9 y10 y11 y12 y13 y14 y15 y16

 

Такими таблицами удобно описывать функционирование различных логических элементов и узлов компьютера.

Рассмотрим различные логические функции yj двух переменных, представленные в таблице не в порядке их нумерации, а в той последовательности, которая позволит выявить их общие и наиболее характерные свойства.

1. Функции y1 и y16 являются, как и функции y0 и y3 для одной переменной, соответственно тождественно равными 0 и 1: y0 º 0; y16 º 1.

2. Функции y11 и y13, как и функция y1 для одной переменной, повторяют соответственно переменные x2 и x1: y11 º x2; y13 º x1.

3. Функции y4 и y6, как и функция y2 для одной переменной, являются соответственно отрицаниями переменных x1 и x2: y4 = 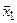; y6 = .

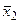4. Функция y9 – конъюнкция (логическое умножение, или операция И) переменных x1, х2, которая обращается в единицу только в том случае, если аргументы x1 и х2 одновременно равны единице, и в нуль – во всех остальных случаях, т. е. если хотя бы один аргумент равен нулю. Иными словами, функция конъюнкции равна min(x1,х2). Обозначается конъюнкция знаком "Ù", который читается как «и». Значение конъюнкции для заданных аргументов находится по правилам логического умножения:

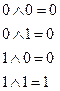
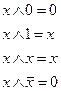
В общем случае, функцию конъюнкции можно определить для любого числа аргументов, т.е. x1 Ù x2 Ù x3 Ù... . Знак "Ù" может быть опущен или заменен точкой, т.е. выражения

x1 x2 x3 ...

или

x1 × x2 × x3 ...

эквивалентны.

Для обозначения операции конъюнкции используется также символ "&".

5. Функция y15 – дизъюнкция (логическое сложение, или операция ИЛИ) обращается в нуль только в том случае, если аргументы x1 и x2 одновременно равны нулю, и в единицу, если хотя бы один аргумент равен единице. Иными словами, функция дизъюнкции равна max(x1,x2). Обозначается дизъюнкция знаком "Ú", который читается как «или». Значение дизъюнкции для заданных аргументов находится по правилам логического сложения:

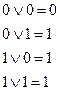
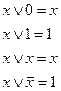
В общем случае, функцию дизъюнкции можно определить для любого числа аргументов, т.е. x1 Ú x2 Ú x3 Ú... .

6. Функция y8 – отрицание конъюнкции (операция И-НЕ), т.е. 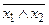. Данная функция обращается в нуль только в том случае, если аргументы x1 и x2 одновременно равны единице, и в единицу, если хотя бы один из аргументов равен нулю:

.

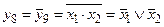Эту функцию называют также «штрих Шеффера».

7. Функция y2 – отрицание дизъюнкции (операция ИЛИ-НЕ), т.е. 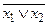. Данная функция обращается в единицу только в том случае, если аргументы x1 и x2 одновременно равны нулю, во всех остальных случаях она равна нулю:

.

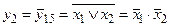Эту функцию называют также «стрелка Пирса».

8. Функция y10 – эквивалентность (или равнозначность) переменных x1 и x2. Данная функция обращается в единицу в том случае, если совпадают значения аргументов x1 и x2; в остальных случаях она равна нулю. Обозначается эквивалентность знаком "~", который читается «равнозначно»:

.

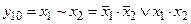9. Функция y7 – отрицание эквивалентности (или неравнозначность) переменных x1 и x2. Запись 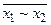читается как «x1 неравнозначно x2». Эта функция равна 1 только в том случае, если значения x1 и x2 не равны. Можно убедиться в том, что значение функции неравнозначности получается поразрядным сложением двоичных переменных x1 и x2 по модулю 2, т. е. без учета переносов в старший разряд.

.

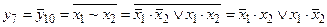Функция y7 более известна как операция «исключающее ИЛИ» и обозначается символом "Å".

10. Функция y12 – импликацияx1 в x2, которая обращается в нуль только в том случае, если переменная x1 равна единице, а x2 – нулю; в остальных случаях функция импликации x1 в x2 равна единице. Данная функция обозначается x1 ® x2 и читается как «если x1, то x2».

.

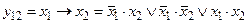11. Функция y14 – импликацияx2 в x1, которая обращается в нуль только в том случае, если переменная x2 равна единице, а x1 – нулю; в остальных случаях функция импликации x2 в x1 равна единице. Данная функция обозначается x2 ® x1 и читается как «если x2, то x1»:

.

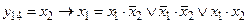12. Функция y5 – отрицание импликации x1 в x2, т. е. 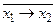. Данную функцию можно рассматривать как функцию запрета со стороны входной переменной x2. Это означает, что выходная функция обращается в 1 только в том случае, если входная переменная x1 равна единице, а x2 – нулю; в остальных случаях функция импликации x1 в x2 равна нулю:

.

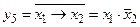13. Функция y3 – отрицание импликацииx2 в x1, т. е. 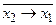. Эта функция обращается в 1 только в том случае, если переменная x2 равна единице, а x1 – нулю, в остальных случаях функция импликации x2 в x1 равна нулю:

.

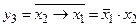Рассмотренное табличное представление логических функций существенно усложняется с увеличением числа аргументов, например для трех аргументов будет 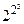= 256 логических функций. В этом случае, особенно при анализе и синтезе логических устройств компьютера, более удобным является аналитическое представление логических функций с помощью нормальных форм.

Наиболее распространенными формами являются дизъюнктивная нормальная форма и конъюнктивная нормальная форма. Если в этих функциях конъюнкции или дизъюнкции содержат все без исключения переменные в прямом или инверсном значении, то та­кая форма функций называется совершенной.

При дизъюнктивной нормальной форме записи наборы переменных, на которых функция принимает значение 1, записываются как конъюнкции (логи­ческое умножение) и связываются знаками логического сложения.

При такой форме записи функции y9 и y15 записываются в следующем виде:

y9 = x1×x2; ;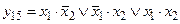

При конъюнктивной нормальной форме записи наборы переменных, на которых функция принимает значение 0, записываются как конъюнкции (логи­ческое сложение) и связываются знаками логического умножения.

Для этой формы записи: