Задачи, приводящие к уравнениям эллиптического типа. Постановка краевых задач

Тема. Уравнения эллиптического типа. Задачи, приводящие к уравнениям эллиптического типа. Фундаментальные решения уравнения Лапласа. Решение задачи Дирихле для круга.

Л Е К Ц И И 13 - 14

 

 

1. Стационарное температурное поле. Ранее мы получили, что температура нестационарного теплового поля удовлетворяет дифференциальному уравнению теплопроводности 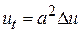. Если процесс стационарен, то устанавливается распределение температуры , не меняющееся с течением времени и, следовательно, удовлетворяющее уравнению Лапласа

 

. (1)

 

При наличии источников тепла получаем уравнение

 

. (2)

 

Неоднородное уравнение Лапласа (2) называют уравнением Пуассона.

Рассмотрим некоторый объем T, ограниченный поверхностью S. Задача о стационарном распределении температуры внутри тела T формулируется следующим образом:

Найти функцию , удовлетворяющую внутри T уравнению

 

 

и граничному условию, которое может быть взято в одном из следующих видов:

 

I		на S	(первая краевая задача)
II		на S	(вторая краевая задача)
III		на S	(третья краевая задача)

где - заданные функции, - производная по внешней нормали к поверхности S. Физический смысл этих граничных условий очевиден. Первую краевую задачу для уравнения Лапласа часто называют задачей Дирихле, а вторую задачу - задачей Неймана.

Если ищется решение в области T внутренней (или внешней) по отношению к поверхности S, то соответствующую задачу называют внутренней (или внешней) краевой задачей.

2. Потенциальное течение жидкости. Пусть внутри некоторого объема T с границей S имеет место стационарное течение несжимаемой жидкости (плотность r = const), характеризуемое скоростью . Если течение жидкости не вихревое, то скорость v является потенциальным вектором, то есть,

 

v = -grad j, (3)

 

где j - скалярная функция, называемая потенциалом скорости. Если отсутствуют источники, то

 

div v = 0. (4)

 

Подставляя сюда выражение (3) для v, получим:

 

div grad j = 0

 

или

 

, (5)

 

т.е. потенциал скорости удовлетворяет уравнению Лапласа.